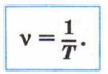|
|
|
|
|
Глава 2. Звуковые явления Колебательное движениеВыведем маятник из положения равновесия, оттянув груз вправо. Пружина деформируется, и в ней возникнет сила упругости 4. Введём величины, характеризующие колебательное движение.
Смещение обычно обозначают буквой х.
Амплитуду обозначают буквой А (см. рис. 117, г). Основной единицей смещения и амплитуды является метр (1 м). Пусть маятник начал движение из точки 1 (см. рис. 117, б), дошёл до точки 2 (см. рис. 117, б) и вернулся обратно в точку 1. В этом случае говорят, что маятник совершил одно полное колебание.
Период обозначают буквой Т и измеряют в секундах (1 с). Важной характеристикой колебательного движения является частота.
Частоту обозначают буквой ν (греч. буква «ню»). Чем больше колебаний совершает маятник за 1 с, тем больше его частота, и наоборот. Единицей частоты является Частота и период колебаний связаны между собой. Например, если маятник за 5 с совершил 10 полных колебаний, то частота колебаний равна 10 : 5 с = 2 (Гц). Период колебаний равен 5 с : 10 = 0,5 с. Таким образом,
|
|
|



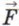 ynp, направленная к положению равновесия (рис. 117, б). Эта сила будет возвращать маятник в положение равновесия (рис. 117, в), которое он пройдёт благодаря инертности и отклонится влево (рис. 117, г). В этой точке в пружине вновь возникнет сила упругости, которая возвратит маятник в положение равновесия. Процесс будет повторяться.
ynp, направленная к положению равновесия (рис. 117, б). Эта сила будет возвращать маятник в положение равновесия (рис. 117, в), которое он пройдёт благодаря инертности и отклонится влево (рис. 117, г). В этой точке в пружине вновь возникнет сила упругости, которая возвратит маятник в положение равновесия. Процесс будет повторяться.
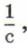 и называют её герц (1 Гц).
и называют её герц (1 Гц).