|
|
|
|
|
Глава 2. Механические свойства жидкостей, газов и твёрдых тел § 10. Сообщающиеся сосудыКак рассчитать давление жидкости на дно сосуда? Какие сосуды являются сообщающимися? 1. Свойство жидкости передавать давление по всем направлениям без изменения позволяет объяснить устройство сообщающихся сосудов.
Примером сообщающихся сосудов может служить жидкостный манометр. Самыми простыми сообщающимися сосудами являются чайник, лейка, кофейник (рис. 27), шлюз.
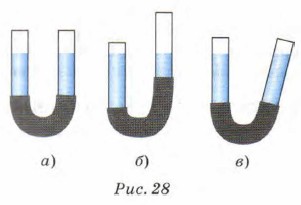
Если взять две стеклянные трубки и соединить их резиновой трубкой (рис. 28, а), то получатся сообщающиеся сосуды. Наливая воду в правую трубку, увидим, что вода будет перетекать и в левую трубку. При этом уровни воды в трубках будут всё время одинаковы. Поднимем правую трубку выше левой (ppic. 28, б). Увидим, что относрхтельно верхнего конца правой трубки уровень воды понизится, а относительно верхнего конца левой трубки — повысится. Однако друг относительно друга уровни останутся одинаковыми, т. е. будут лежать в одной и той же горизонтальной плоскости.
Наклоним правую трубку, оставив левую в вертикальном положении (рис. 28, в). Вода в правой трубке установится горизонтально и уровни воды в трубках останутся одинаковыми. Если трубки заполнить другой жидкостью, например маслом, керосином или ртутью, то всё равно уровни жидкости в трубках будут одинаковы.
Это верно при условии, что давление на поверхность жидкости в обоих сосудах одинаково. Как вы уже знаете, именно по разности уровней жидкости в трубках жидкостного манометра можно судить о значении давления. 2. Объяснить полученный вывод можно следующим образом. Жидкость в сосудах не перемещается, следовательно, значения давления её в сосудах на одном уровне, в том числе и на дно, одинаковы. Жидкость имеет одинаковую плотность, поскольку она однородная. Следовательно, в соответствии с формулой р = ρgh высоты жидкости должны быть одинаковы.
|
|
|