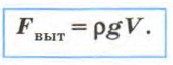|
|
|
|
|
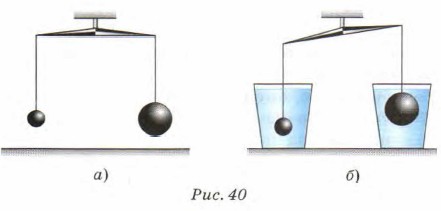
Глава 2. Механические свойства жидкостей, газов и твёрдых тел Действие жидкости и газа на погружённое в них тело4. Заменим один из шариков на шарик большего объёма, но такой же массы (рис. 40, а). Уравновесим их и опустим в сосуды с водой. Заметим, что равновесие также нарушится. Конец рычага, к которому подвешено тело большего объёма, поднимется вверх (рис. 40, б). Следовательно, выталкивающая сила тем больше, чем больше объём тела, погружённого в жидкость.
5. Эксперименты показывают, что
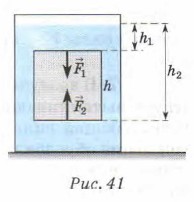
Её можно вычислить по формуле Fвыт = ρgV. 6. Получим формулу для расчёта выталкивающей силы теоретически. Для этого построим модель. Будем считать, что полностью погружённое в жидкость тело имеет форму куба (рис. 41). Также будем считать жидкость несжимаемой и её плотность неизменной во всём объёме.
Пусть длина ребра куба равна h, а площадь его грани S. Как мы уже выяснили, выталкивающая сила Fвыт, равна разности сил давления, действующих на нижнюю F2 и верхнюю F1 грани куба: Fвыт = F2 - F1. Сила F2 равна произведению давления жидкости на нижнюю грань р2 и площади грани S, т. е. F2 = p2S. Сила F1 равна произведению давления жидкости на верхнюю грань р1 и площади грани S, т. е. F1 = p1S. Тогда Fвыт = P2S - P1S = (p2 - p1)S' Давление р1 равно произведению плотности жидкости ρ, ускорения свободного падения g и высоты столба жидкости над верхней гранью куба h1 : р1 = ρgh1. Давление на нижнюю грань куба р2 = ρgh2, где h2 — высота столба жидкости от её поверхности до нижней грани куба. Подставив р1 и р2 в выражение для выталкивающей силы, получим: Fвыт = (ρgh2 - ρgh1)S = ρg(h2 - h1)S = ρghS. Произведение длины ребра куба h и площади его грани S представляет собой объём куба V: V = hS. Откуда:
Произведение pV — масса жидкости в объёме погружённого в неё тела. Произведение массы жидкости (ρV) и ускорения свободного падения g равно силе тяжести, действующей на жидкость. Она в данном случае равна весу жидкости. Таким образом,
|
|
|