Главная >> Физика 9 класс. Генденштейн. Кайдалов

§ 7. Взаимодействия и силы

Сложение сил

Опыты показывают, что в тех случаях, когда размерами тела можно пренебречь, действие на тело нескольких сил можно заменить действием одной силы.

Силу, которая производит на тело такое же действие, как несколько одновременно приложенных к этому телу сил, называют равнодействующей этих сил. Нахождение равнодействующей нескольких сил называют сложением этих сил.

Так как силы являются векторными величинами, то

силы складывают по правилу сложения векторов.

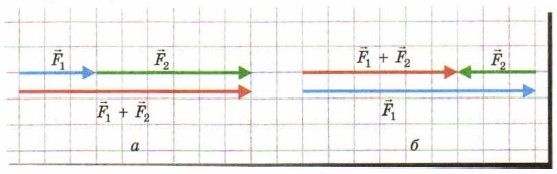
Если две силы направлены одинаково, их равнодействующая направлена так же, а модуль равнодействующей равен сумме модулей сил-слагаемых. На рис. 7.5, а приведен пример сложения таких сил. Силы-слагаемые обозначены синей и зеленой стрелками, а их равнодействующая — красной стрелкой.

Если две не равные по модулю силы направлены противоположно, их равнодействующая направлена в сторону большей силы, а модуль равнодействующей равен разности модулей сил-слагаемых. На рис. 7.5, б приведен пример сложения таких сил.

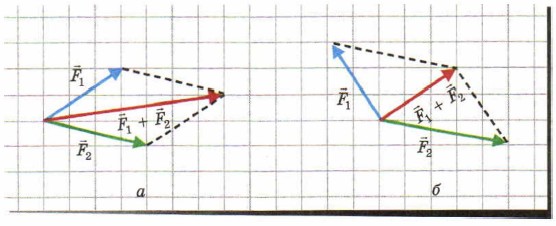
Рис. 7.5. Сложение сил, направленных вдоль одной прямой. Равнодействующая обозначена красной стрелкой

Если силы направлены под углом друг к другу, то их равнодействующую находят, используя сложение векторов по правилу параллелограмма, показанному на рис. 7.6. В этом случае начала двух векторов-слагаемых совмещают и строят параллелограмм, смежными сторонами которого являются векторы-слагаемые. Суммой этих векторов является вектор, совпадающий с диагональю построенного параллелограмма, причем начало этого вектора совпадает с общим началом векторов-слагаемых.

На рис. 7.6, а приведен пример сложения сил, когда угол между силами-слагаемыми острый, а на рис. 7.6, б — когда этот угол тупой.

Рис. 7.6. Сложение сил, направленных под углом. Равнодействующая обозначена красной стрелкой

Как мы уже знаем,

если равнодействующая двух сил равна нулю, то эти силы равны по модулю и направлены противоположно.