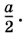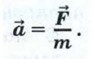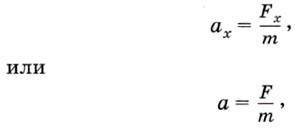|
|
|
|
|
Глава 1. Законы взаимодействия и движения тел § 11. Второй закон НьютонаИз курса физики 7 класса вам известно, что причиной изменения скорости тела, а значит, и причиной возникновения ускорения является действие на это тело других тел с некоторой силой.
Когда на тело действует сразу несколько сил, то оно движется с ускорением, если равнодействующая F этих сил не равна нулю. Напомним, что равнодействующей нескольких сил, одновременно приложенных к телу, называется сила, производящая на тело такое же действие, как все эти силы вместе. Поскольку ускорение возникает в результате действия силы, то естественно предположить, что существует количественная взаимосвязь между этими величинами. Жизненный опыт убеждает нас в том, что чем больше будет равнодействующая приложенных к телу сил, тем большее ускорение получит при этом тело. Например, чем сильнее футболист бьёт ногой по лежащему на поле мячу, тем большее ускорение приобретает при этом мяч и тем бо́льшую скорость он успевает набрать за те доли секунды, пока взаимодействует с ногой футболиста (о приобретённой мячом скорости можно судить по тому, насколько далеко он отлетает после удара). Многочисленные наблюдения и опыты свидетельствуют также о том, что ускорения, получаемые телами, зависят от массы этих тел.
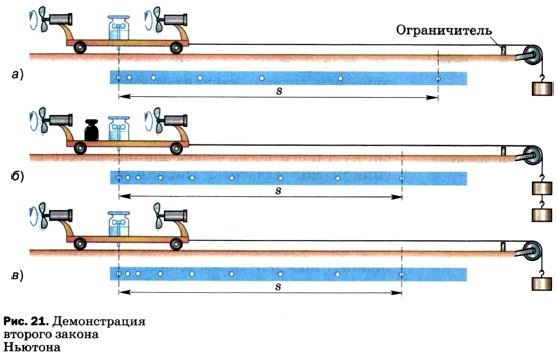
Чтобы в этом удостовериться, проделаем опыт. Возьмём два одинаковых воздушных шарика. В один из них вложим маленькую бусинку такого веса, чтобы шарик вместе с бусинкой мог взлететь. Наполним оба шарика гелием до одного и того же объёма. Расположим шарики на одной и той же высоте (ближе к полу) и отпустим. Мы увидим, что шарик с бусинкой достигнет потолка позже (рис. 20). Значит, под действием одной и той же равнодействующей силы F, равной разности действующих на шарики архимедовой силы и силы сопротивления воздуха (F = FA - Fconp), шарик без груза получил большее ускорение. О величине его ускорения можно судить по тому, что одно и то же расстояние — от места старта до потолка — он прошёл за меньший промежуток времени, чем шарик с бусинкой, масса которого больше. Значит, его скорость росла быстрее, что свидетельствует о большем ускорении движения. Для подтверждения того, что при данной силе получаемое телом ускорение зависит от массы этого тела, рассмотрим ещё один опыт. На рисунке 21, а изображена легкоподвижная тележка с укреплёнными на ней маленькой капельницей и двумя одинаковыми лёгкими вентиляторами (работающими от находящейся внутри каждого из них батарейки одной и той же мощности). Допустим, масса тележки вместе с капельницей и вентиляторами нам известна. К тележке привязан один из концов нити, перекинутой через блок. К другому концу нити прикреплён небольшой груз. Этот груз нужен для того, чтобы скомпенсировать силу трения, действующую на движущуюся тележку.
Вдоль траектории движения тележки расположим бумажную ленту. Откроем кран и включим вентиляторы. В результате взаимодействия их винтов с воздухом вентиляторы будут толкать тележку с некоторой постоянной силой по направлению к ограничителю на краю стола. При этом на бумажной ленте будут оставаться следы капель, падающих через равные промежутки времени Т. После того как тележка остановится, выключим вентиляторы. Измерив расстояния между соседними метками на ленте, можно убедиться в том, что эти расстояния относятся как ряд нечётных последовательных чисел (1 : 3 : 5 : 7 : 9...). Значит, под действием постоянной силы тележка двигалась равноускоренно. Чтобы определить ускорение движения тележки, измерим модуль (s) вектора её перемещения (т. е. расстояние между крайними метками на ленте). Затем посчитаем число (n) промежутков между соседними метками на ленте, или, что то же самое, число промежутков времени Т за время движения тележки. По формуле t = Тn вычислим промежуток времени t, за который тележка переместилась на расстояние s. Из формулы Теперь удвоим массу всей движущейся системы (состоящей из тележки с вентиляторами и капельницей и груза на нити) с помощью гирь, как показано на рисунке 21, (б) (при этом одна гирька добавляется к уже имеющемуся грузу на конце нити для компенсации возросшей силы трения). Повторим опыт. Определив ускорение и сравнив его с ускорением в предыдущем опыте, можно убедиться в том, что при действии одной и той же силы система тел, масса которой стала вдвое больше, приобрела в 2 раза меньшее ускорение, т. е. Из рассмотренного опыта и ряда подобных следует, что ускорения, сообщаемые телам одной и той же постоянной силой, обратно пропорциональны массам этих тел. С помощью этой же экспериментальной установки можно провести опыт, позволяющий установить количественную взаимосвязь между ускорением и силой, сообщающей телу это ускорение. Для этого снимем добавленные в предыдущем опыте гири, чтобы масса системы опять стала такой, как в первом опыте (рис. 21, в). Но теперь приведём тележку в движение, включив только один вентилятор, в результате чего на тележку будет действовать в 2 раза меньшая сила, чем при двух включённых вентиляторах (придававших тележке ускорение а). Как показывают измерения и вычисления, при уменьшении силы в 2 раза ускорение тоже уменьшается в 2 раза, т. е. становится равным
Значит, ускорение, с которым движется тело постоянной массы, прямо пропорционально приложенной к этому телу силе, в результате которой возникает ускорение. Количественная взаимосвязь между массой тела, ускорением, с которым оно движется, и равнодействующей приложенных к телу сил, вызывающих это ускорение, называется вторым законом Ньютона. Он формулируется так:
Следует помнить, что во втором законе Ньютона, так же как и в первом, под телом подразумевается материальная точка, движение которой рассматривается в инерциальной системе отсчёта. Математически второй закон Ньютона записывается так:
Из формулы следует, что вектор ускорения совпадает по направлению с вектором равнодействующей приложенных к телу сил. В скалярном виде второй закон Ньютона можно записать:
где аx и Fx — проекции векторов ускорения и силы на ось X, а а и F — модули этих векторов. Вам уже известно, что сила измеряется в ньютонах (Н). Покажем, как с помощью второго закона Ньютона даётся определение единицы силы — 1 Н. Для этого выразим модуль силы: F = mа. В соответствии с этой формулой сила равна единице (1 Н), если масса равна единице (1 кг) и ускорение равно единице (1 м/с2). В СИ за единицу силы принимается сила, сообщающая телу массой 1 кг ускорение 1 м/с2 в направлении действия силы. Получим соотношение между единицами силы, массы и ускорения: 1 Н = 1 кг • 1 м/с2 = 1 кг • м/с2. Вопросы1. Что является причиной ускоренного движения тел?
Упражнение 111. Определите силу, под действием которой велосипедист скатывается с горки с ускорением, равным 0,8 м/с2, если масса велосипедиста вместе с велосипедом равна 50 кг. 2. Через 20 с после начала движения электровоз развил скорость 4 м/с. Найдите силу, сообщающую ускорение, если масса электровоза равна 184 т. 3. Два тела равной массы движутся с ускорениями 0,08 и 0,64 м/с2 соответственно. Равны ли модули действующих на тела сил? Чему равна сила, действующая на второе тело, если на первое действует сила 1,2 Н? 4. С каким ускорением будет всплывать находящийся под водой мяч массой 0,5 кг, если действующая на него сила тяжести равна 5 Н, архимедова сила — 10 Н, а средняя сила сопротивления движению — 2 Н? 5. Баскетбольный мяч, пройдя сквозь кольцо и сетку, под действием силы тяжести сначала движется вниз с возрастающей скоростью, а после удара о пол — вверх с уменьшающейся скоростью. Как направлены векторы ускорения, скорости и перемещения мяча по отношению к силе тяжести при его движении вниз; вверх? 6. Тело движется прямолинейно с постоянным ускорением. Какая величина, характеризующая движение этого тела, всегда сона- правлена с равнодействующей приложенных к телу сил, а какие величины могут быть направлены противоположно равнодействующей?
|
|
|





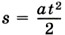 выразим модуль ускорения
выразим модуль ускорения 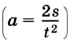 и рассчитаем его.
и рассчитаем его.