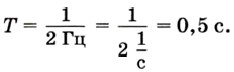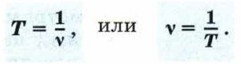|
|
|
|
|
Глава 2. Механические колебания и волны. Звук § 24. Величины, характеризующие колебательное движениеСравним колебания двух одинаковых маятников, изображённых на рисунке 58. Первый маятник колеблется с большим размахом, т. е. его крайние положения находятся дальше от положения равновесия, чем у второго маятника.
Будем рассматривать колебания, происходящие с малыми амплитудами (рис. 59), при которых длину дуги Амплитуда колебаний пружинного маятника (см. рис. 53) равна длине отрезка ОВ или ОА. Колеблющееся тело совершает одно полное колебание, если от начала колебаний проходит путь, равный четырём амплитудам. Например, переместившись из точки О1 в точку В1, затем в точку А1 и вновь в точку O1 (см. рис. 58), шарик совершает одно полное колебание.
Период колебаний обозначается буквой Т и в СИ измеряется в секундах (с). Подвесим два одинаковых шарика на нитях разной длины и приведём их в колебательное движение. Увидим, что за один и тот же промежуток времени короткий маятник совершит больше колебаний, чем длинный.
Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц). Допустим, в одну секунду маятник совершает два колебания, т. е. частота его колебаний равна 2 Гц
Таким образом, период колебания Т и частота колебаний ν связаны следующей зависимостью:
На примере колебаний маятников разной длины приходим к выводу: частота и период свободных колебаний нитяного маятника зависят от длины его нити. Чем больше длина нити маятника, тем больше период колебаний и меньше частота. (Эту зависимость вы будете исследовать при выполнении лабораторной работы № 3.)
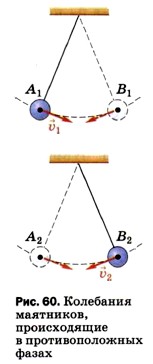
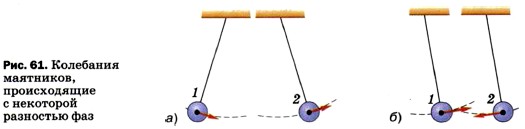
Не только нитяной маятник, но и любая другая колебательная система имеет определённую собственную частоту, зависящую от параметров этой системы. Например, собственная частота пружинного маятника зависит от массы груза и жёсткости пружины. Рассмотрим колебания двух одинаковых маятников (рис. 60). В один и тот же момент времени левый маятник из крайнего левого положения начинает движение вправо, а правый маятник из крайнего правого положения движется влево. Оба маятника колеблются с одной и той же частотой (поскольку длины их нитей равны) и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости маятников направлены, в противоположные стороны. В таком случае говорят, что колебания маятников происходят в противоположных фазах. Маятники, изображённые на рисунке 58, тоже колеблются с одинаковыми частотами. Скорости этих маятников в любой момент времени направлены одинаково. В этом случае говорят, что маятники колеблются в одинаковых фазах. Рассмотрим ещё один случай. В момент, изображённый на рисунке 61, (а), скорости обоих маятников направлены вправо. Но через некоторое время (рис. 61, б) они будут направлены в разные стороны. В таком случае говорят, что колебания происходят с определённой разностью фаз.
Физическая величина, называемая фазой, используется не только при сравнении колебаний двух или нескольких тел, но и для описания колебаний одного тела. Формула для определения фазы в любой момент времени будет рассмотрена в старших классах. Таким образом, колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой. Вопросы1. Что называется амплитудой колебаний; периодом колебаний; частотой колебаний? В каких единицах измеряется каждая из этих величин?
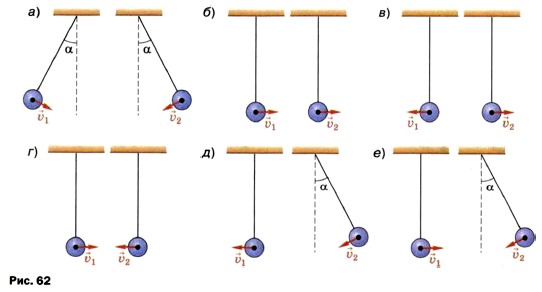
Упражнение 241. На рисунке 62 изображены пары колеблющихся маятников. В каких случаях два маятника колеблются: в одинаковых фазах по отношению друг к другу; в противоположных фазах? 2. Частота колебаний стометрового железнодорожного моста равна 2 Гц. Определите период этих колебаний.
3. Период вертикальных колебаний железнодорожного вагона равен 0,5 с. Определите частоту колебаний вагона. 4. Игла швейной машины делает 600 полных колебаний в минуту. Какова частота колебаний иглы? 5. Амплитуда колебаний груза на пружине равна 3 см. Какой путь от положения равновесия пройдёт груз за время, равное ¼ Т; ½ Т; ¾ Т; Т? 6. Амплитуда колебаний груза на пружине равна 10 см, частота 0,5 Гц. Какой путь пройдёт груз за 2 с? ЗаданиеСпланируйте эксперимент с участием магнитных сил, имитирующих увеличение ускорения свободного падения и действующих на колеблющийся нитяной маятник. Проведите этот эксперимент и сделайте вывод о качественной зависимости периода колебаний от ускорения свободного падения.
|
|
|



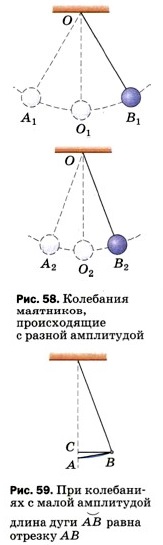
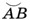 можно считать равной отрезку АВ и даже полухорде СВ. Поэтому под амплитудой колебаний нитяного маятника можно понимать как дугу, так и любой из этих отрезков. Так, амплитуда колебаний первого маятника (см. рис. 58) равна О1А1 или O1В1, а второго — О2A2 или O2В2. Амплитуду обозначают буквой А ив СИ измеряют в единицах длины — метрах (м), сантиметрах (см) и др. Амплитуду можно измерять также в единицах плоского угла, например в градусах, поскольку дуге окружности соответствует определённый центральный угол, т. е. угол с вершиной в центре окружности (в данном случае в точке О).
можно считать равной отрезку АВ и даже полухорде СВ. Поэтому под амплитудой колебаний нитяного маятника можно понимать как дугу, так и любой из этих отрезков. Так, амплитуда колебаний первого маятника (см. рис. 58) равна О1А1 или O1В1, а второго — О2A2 или O2В2. Амплитуду обозначают буквой А ив СИ измеряют в единицах длины — метрах (м), сантиметрах (см) и др. Амплитуду можно измерять также в единицах плоского угла, например в градусах, поскольку дуге окружности соответствует определённый центральный угол, т. е. угол с вершиной в центре окружности (в данном случае в точке О).
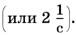 Чтобы найти период колебания, необходимо одну секунду разделить на число колебаний в эту секунду, т. е. на частоту:
Чтобы найти период колебания, необходимо одну секунду разделить на число колебаний в эту секунду, т. е. на частоту: