Главная >> Физика 9 класс. Перышкин. Онлайн учебник

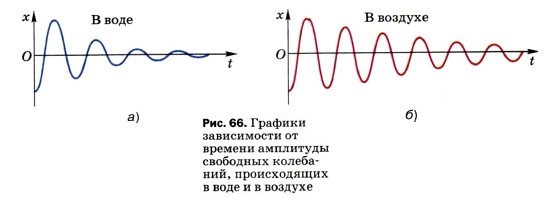
Глава 2. Механические колебания и волны. Звук

§ 26. Затухающие колебания. Вынужденные колебания

Обратимся ещё раз к рисунку 53. Перемещая шарик из точки О (положения равновесия) в точку В, мы растягиваем пружину. При этом мы совершаем некоторую работу по преодолению силы её упругости, благодаря чему пружина приобретает потенциальную энергию. Если теперь отпустить шарик, то по мере его приближения к точке О деформация пружины и потенциальная энергия маятника будут уменьшаться, а скорость и кинетическая энергия — увеличиваться.

Допустим, что потери энергии на преодоление сил трения при движении маятника пренебрежимо малы. Тогда, согласно закону сохранения энергии, полную механическую энергию маятника (т. е. Е_п + Е_к) в любой момент времени можно считать одинаковой и равной той потенциальной энергии, которую мы изначально сообщили пружине, растянув её на длину отрезка ОВ. При этом маятник мог бы совершать колебания сколь угодно долго с постоянной амплитудой, равной ОВ.

Так было бы, если бы при движении не было никаких потерь энергии.

Но реально потери энергии всегда есть. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха, переходя при этом во внутреннюю энергию. Амплитуда колебаний постепенно уменьшается, и через некоторое время колебания прекращаются. Такие колебания называются затухающими (рис. 66).

Чем больше силы сопротивления движению, тем быстрее прекращаются колебания. Например, в воде колебания затухают быстрее, чем в воздухе (рис. 66, а, б).

До сих пор рассматривались свободные колебания, т. е. колебания, происходящие за счёт начального запаса энергии.

Свободные колебания всегда затухающие, так как весь запас энергии, первоначально сообщённый колебательной системе, в конце концов уходит на совершение работы по преодолению сил трения и сопротивления среды (т. е. механическая энергия переходит во внутреннюю). Поэтому свободные колебания почти не имеют практического применения.

Чтобы колебания были незатухающими, необходимо восполнять потери энергии за каждый период колебаний. Это можно осуществить, воздействуя на колеблющееся тело периодически изменяющейся силой. Например, каждый раз подталкивая качели в такт их колебаниям, можно добиться того, чтобы колебания не затухали.

• Колебания, совершаемые телом под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями.

Внешняя периодически изменяющаяся сила, вызывающая эти колебания, называется вынуждающей силой.

Если на покоящиеся качели начать действовать периодически меняющейся вынуждающей силой, то в течение некоторого времени амплитуда вынужденных колебаний качелей будет возрастать, т. е. амплитуда каждого последующего колебания будет больше, чем предыдущего. Увеличение амплитуды прекратится тогда, когда энергия, теряемая качелями на преодоление силы трения, станет равна энергии, получаемой ими извне (за счёт работы вынуждающей силы).

В большинстве случаев постоянная частота вынужденных колебаний устанавливается не сразу, а спустя некоторое время после их начала.

Когда амплитуда и частота вынужденных колебаний перестают меняться, говорят, что колебания установились.

Частота установившихся вынужденных колебаний равна частоте вынуждающей силы.

Вынужденные колебания могут совершать даже тела, которые не являются колебательными системами, например, игла швейной машины, поршни в двигателе внутреннего сгорания и многие другие. Колебания таких тел тоже происходят с частотой вынуждающей силы.

Вынужденные колебания — незатухающие. Они происходят до тех пор, пока действует вынуждающая сила.

Вопросы

1. Что можно сказать о полной механической энергии колеблющегося маятника в любой момент времени, если допустить, что потерь энергии нет? Согласно какому закону это можно утверждать?
2. Как меняется с течением времени амплитуда свободных колебаний, происходящих в реальных условиях? В чём причина такого изменения?
3. Где быстрее прекратятся колебания маятника — в воздухе или в воде? Почему? (Начальный запас энергии в обоих случаях одинаков.)
4. Могут ли свободные колебания быть незатухающими? Почему? Что необходимо делать для того, чтобы колебания были незатухающими?
5. Что можно сказать о частоте установившихся вынужденных колебаний и частоте вынуждающей силы?
6. Могут ли тела, не являющиеся колебательными системами, совершать вынужденные колебания? Приведите примеры.
7. До каких пор происходят вынужденные колебания?

Упражнение 26

1. Горизонтальный пружинный маятник, изображённый на рисунке 53, отвели в сторону и отпустили. Как меняются перечисленные в таблице 1 величины при движении маятника на указанных участках его пути? Перечертите таблицу в тетрадь и заполните её.

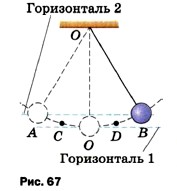
2. На рисунке 67 изображён шарик на нити, колеблющийся без трения между точками А и В. Находясь в точке В, этот маятник обладает потенциальной энергией, равной 0,01 Дж относительно горизонтали 1, принятой за нулевой уровень отсчёта потенциальной энергии. Чему равна: а) потенциальная энергия шарика в точках А и О; б) кинетическая энергия шарика в точках В, О и А; в) полная механическая энергия шарика в точках В, D,O,C и А?

3. Рассмотрите рисунок 56 и скажите, какие из тел способны совершать: свободные колебания; вынужденные колебания. Ответ обоснуйте.

4. Могут ли происходить: а) вынужденные колебания в колебательной системе; б) свободные колебания в системе, не являющейся колебательной? Приведите примеры.