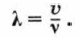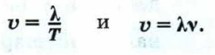|
|
|
|
|
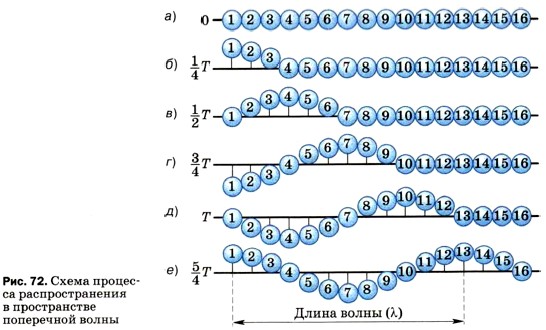
Глава 2. Механические колебания и волны. Звук § 29. Длина волны. Скорость распространения волнРассмотрим более подробно процесс передачи колебаний от точки к точке при распространении поперечной волны. Для этого обратимся к рисунку 72, на котором показаны различные стадии процесса распространения поперечной волны через промежутки времени, равные 1/4 Т. На рисунке 72, (а) изображена цепочка пронумерованных шариков. Это модель: шарики символизируют частицы среды. Будем считать, что между шариками, как и между частицами среды, существуют силы взаимодействия, в частности при небольшом удалении шариков друг от друга возникает сила притяжения.
Если привести первый шарик в колебательное движение, т. е. заставить его двигаться вверх и вниз от положения равновесия, то благодаря силам взаимодействия каждый шарик в цепочке будет повторять движение первого, но с некоторым запаздыванием (сдвигом фаз). Это запаздывание будет тем больше, чем дальше от первого шарика находится данный шарик. Так, например, видно, что четвёртый шарик отстаёт от первого на 1/4 колебания (рис. 72, б). Ведь когда первый шарик прошёл 1/4 часть пути полного колебания, максимально отклонившись вверх, четвёртый шарик только начинает движение из положения равновесия. Движение седьмого шарика отстаёт от движения первого на 1/2 колебания (рис. 72, в), десятого — на 3/4 колебания (рис. 72, г). Тринадцатый шарик отстаёт от первого на одно полное колебание (рис. 72, д), т. е. находится с ним в одинаковых фазах. Движения этих двух шариков совершенно одинаковы (рис. 72, е).
Длина волны обозначается греческой буквой λ («ламбда»). Расстояние между первым и тринадцатым шариками (см. рис. 72, е), вторым и четырнадцатым, третьим и пятнадцатым и так далее, т. е. между всеми ближайшими друг к другу шариками, колеблющимися в одинаковых фазах, будет равно длине волны λ. Из рисунка 72 видно, что колебательный процесс распространился от первого шарика до тринадцатого, т. е. на расстояние, равное длине волны λ, за то же время, за которое первый шарик совершил одно полное колебание, т. е. за период колебаний Т. Значит,
где Поскольку период колебаний связан с их частотой зависимостью
Таким образом, длина волны зависит от частоты (или периода) колебаний источника, порождающего эту волну, и от скорости распространения волны. Из формул для определения длины волны можно выразить скорость волны:
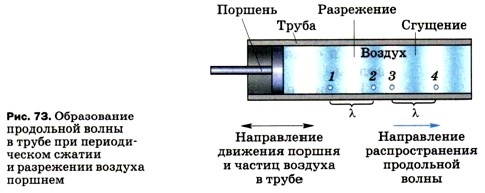
Формулы для нахождения скорости волны справедливы как для поперечных, так и для продольных волн. Длину волны λ при распространении продольных волн можно представить с помощью рисунка 73. На нём изображена (в разрезе) труба с поршнем. Поршень совершает колебания с небольшой амплитудой вдоль трубы. Его движения передаются прилегающим к нему слоям воздуха, заполняющего трубу. Колебательный процесс постепенно распространяется вправо, образуя в воздухе разрежения и сгущения.
На рисунке даны примеры двух отрезков, соответствующих длине волны λ. Очевидно, что точки 1 и 2 являются ближайшими друг к другу точками, колеблющимися в одинаковых фазах. То же самое можно сказать про точки 3 и 4. Вопросы1. Что называется длиной волны?
Упражнение 271. С какой скоростью распространяется волна в океане, если длина волны равна 270 м, а период колебаний равен 13,5 с? 2. Определите длину волны при частоте 200 Гц, если скорость распространения волны равна 340 м/с. 3. Лодка качается на волнах, распространяющихся со скоростью 1,5 м/с. Расстояние между двумя ближайшими гребнями волн равно 6 м. Определите период колебаний лодки.
|
|
|



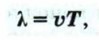
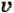 — скорость волны.
— скорость волны.
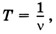 то длина волны может быть выражена через скорость волны и частоту:
то длина волны может быть выражена через скорость волны и частоту: