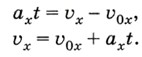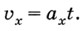|
|
|
|
|
Глава 1. Законы взаимодействия и движения тел § 6. Скорость прямолинейного равноускоренного движения. График скоростиВам известно, что при прямолинейном равноускоренном движении проекцию вектора ускорения на ось X можно найти по формуле:
Выразим из этой формулы проекцию
Если в начальный момент тело покоилось, т. е.
Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика. Из курса математики вам известна линейная функция у = kx + b, где х — аргумент, k — постоянный коэффициент, b — свободный член. Графиком этой функции является прямая. Функция
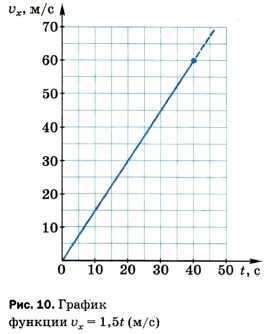
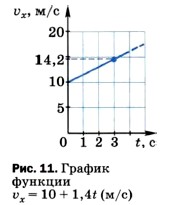
Построим, например, график зависимости от времени проекции вектора скорости разгоняющегося перед взлётом самолёта, который движется из состояния покоя прямолинейно с ускорением 1,5 м/с2 в течение 40 с. Сонаправим ось X со скоростью движения самолёта. Тогда проекции векторов скорости и ускорения будут положительны. Для построения заданной прямой достаточно знать координаты (т. е. t и Например, при t0 = 0 Теперь построим аналогичный график для случая, когда начальная скорость не равна нулю (при том, что модуль скорости, как и в предыдущем примере, возрастает). Для этого воспользуемся таким примером. По дороге едет автомобиль со скоростью 10 м/с (36 км/ч). Водитель автомобиля, увидев дорожный знак, снимающий ограничение скорости, нажал на педаль газа, в результате чего автомобиль стал двигаться с постоянным ускорением 1,4 м/с2. Построим график зависимости от времени проекции вектора мгновенной скорости на ось X, сонаправленную со скоростью прямолинейно движущегося автомобиля, для первых четырёх секунд разгона.
В этом случае зависимость График, построенный по этим точкам, представлен на рисунке 11. Он отсекает на оси Построим теперь график зависимости проекции вектора скорости от времени, если начальная скорость не равна нулю, а модуль вектора скорости уменьшается с течением времени.
Допустим, водитель автомобиля, движущегося со скоростью 20 м/с (72 км/ч), нажимает на педаль тормоза. В результате автомобиль движется с ускорением 2 м/с2 и через 10 с останавливается. За начало отсчёта времени примем момент начала торможения, когда скорость автомобиля ещё была равна 20 м/с. В этом случае нет необходимости рассчитывать значение проекции вектора скорости, поскольку координаты двух точек графика очевидны: при t0 = 0 Поскольку скорость уменьшается по модулю, то график образует с положительным направлением оси t тупой угол. Вопросы1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.
Упражнение 61. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с2? 2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с2. Через какой промежуток времени его скорость возрастёт до 2 м/с? 3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось X, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: a)
4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось X, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) 5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямо- линейном движении двух тел. С каким по модулю ускорением движется тело I; тело II?
|
|
|



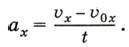
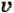 x вектора скорости
x вектора скорости 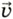 которую имело движущееся тело к концу промежутка времени t, отсчитываемого от момента начала наблюдения, т. е. от t0 = 0:
которую имело движущееся тело к концу промежутка времени t, отсчитываемого от момента начала наблюдения, т. е. от t0 = 0: