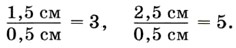|
|
|
|
|
Глава 1. Законы взаимодействия и движения тел § 8. Перемещение тела при прямолинейном равноускоренном движении без начальной скоростиРассмотрим, как рассчитывается проекция вектора перемещения тела, движущегося равноускоренно, если его начальная скорость
будет выглядеть так:
Перепишем это уравнение, подставив в него вместо проекций sx и ах модули s и а векторов перемещения и ускорения. Поскольку в данном случае векторы
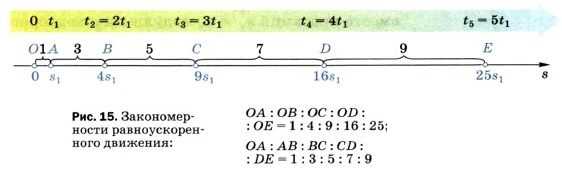
Из этой формулы следует, что при прямолинейном равноускоренном движении без начальной скорости модуль вектора перемещения прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено. Это означает, что при увеличении в n раз времени движения (отсчитываемого от момента начала движения) перемещение увеличивается в n2 раз. Например, если за произвольный промежуток времени t1 от начала движения тело совершило перемещение Эта зависимость модуля вектора перемещения от времени при прямолинейном равноускоренном движении без начальной скорости наглядно отражена на рисунке 15, где отрезки ОА, ОВ, ОС, OD и ОЕ представляют собой модули векторов перемещений (s1, s2, s3, s4 и s5), совершённых телом соответственно за промежутки времени t1, t2 = 2t1, t3 = 3t1, t4 = 4t1 и t5 = 5t1.
Из этого рисунка видно, что ОА : ОВ : ОС : OD : ОЕ = 1 : 4 : 9 : 16 : 25, (1) т. е. при увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1 модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел. Из рисунка 15 видна ещё одна закономерность: ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9, (2) т. е. модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени (каждый из которых равен t1), относятся как ряд последовательных нечётных чисел.
Закономерности (1) и (2) присущи только равноускоренному движению. Поэтому ими можно пользоваться, если необходимо определить, является движение равноускоренным или нет. Определим, например, было ли равноускоренным движение улитки, которая за первые 20 с движения переместилась на 0,5 см, за вторые 20 с — на 1,5 см, за третьи 20 с — на 2,5 см. Для этого найдём, во сколько раз перемещения, совершённые за второй и третий промежутки времени, больше, чем за первый:
Значит, 0,5 см : 1,5 см : 2,5 см = 1 : 3 : 5. Поскольку эти отношения представляют собой ряд последовательных нечётных чисел, то движение тела было равноускоренным. В данном случае равноускоренный характер движения был выявлен на основании закономерности (2). Вопросы1. По каким формулам рассчитываются проекция и модуль вектора перемещения тела при его равноускоренном движении из состояния покоя?
Упражнение 81. Отходящий от станции поезд в течение первых 20 с движется прямолинейно и равноускоренно. Известно, что за третью секунду от начала движения поезд прошёл 2 м. Определите модуль вектора перемещения, совершённого поездом за первую секунду, и модуль вектора ускорения, с которым он двигался. 2*. Автомобиль, двигаясь равноускоренно из состояния покоя, за пятую секунду разгона проходит 6,3 м. Какую скорость развил автомобиль к концу пятой секунды от начала движения? 3*. Некоторое тело за первые 0,03 с движения без начальной скорости переместилось на 2 мм, за первые 0,06 с — на 8 мм, за первые 0,09 с — на 18 мм. На основании закономерности (1) докажите, что в течение всех 0,09 с тело двигалось равноускоренно.
|
|
|



 0 равна нулю. В этом случае уравнение
0 равна нулю. В этом случае уравнение
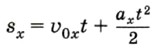
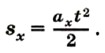
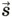 и
и 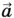 направлены в одну сторону, их проекции имеют одинаковые знаки. Поэтому уравнение для модулей векторов можно записать:
направлены в одну сторону, их проекции имеют одинаковые знаки. Поэтому уравнение для модулей векторов можно записать:
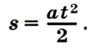
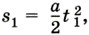 то за промежуток времени t2 = 2t1 (отсчитываемый от того же момента, что и t1) оно совершит перемещение
то за промежуток времени t2 = 2t1 (отсчитываемый от того же момента, что и t1) оно совершит перемещение 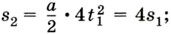 за промежуток времени t3 = 3t1 — перемещение
за промежуток времени t3 = 3t1 — перемещение 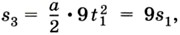 за промежуток времени tn = nt1 — перемещение sn = n2s1 (где n — натуральное число).
за промежуток времени tn = nt1 — перемещение sn = n2s1 (где n — натуральное число).