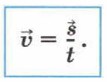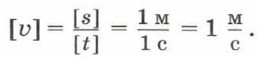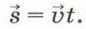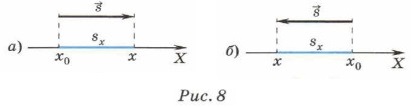|
|
|
|
|
Глава 1. Законы механики § 2. Равномерное прямолинейное движениеКакое движение называют равномерным? Что называют скоростью равномерного движения? Как найти проекцию вектора на координатную ось? 1. Существуют различные виды механического движения. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. При движении скорость тела может оставаться постоянной или с течением времени изменяться. В зависимости от характера изменения скорости движение будет равномерным или неравномерным. Рассмотрим движение, происходящее с постоянной скоростью, траекторией которого является прямая линия, т. е. равномерное прямолинейное движение.
Слова за «любые равные промежутки времени» означают, что, какие бы равные промежутки времени (1с, 2 с, 5 мин, 10 мин и т. д.) мы ни выбрали, перемещение тела за эти равные промежутки времени будет одинаковым. Например, если автомобиль за каждые 2 мин проезжает 1800 м, за каждую 1 мин — 900 м, за каждую 1с — 15 м, то можно считать, что он движется равномерно. Понятно, что практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Поэтому равномерное движение является моделью реального движения. 2. Если сравнивать равномерное движение нескольких тел, можно отметить, что быстрота изменения их положения в пространстве может быть различной. «Быстрота» движения характеризуется физической величиной, называемой скоростью.
Если за время t тело совершило перемещение
Единица скорости в СИ — метр в секунду (1 м/с). Эту единицу можно получить, разделив единицу перемещения на единицу времени:
За единицу скорости принимают скорость такого равномерного движения, при котором тело за 1с совершает перемещение 1 м. Зная скорость равномерного движения, можно найти перемещение тела за любой промежуток времени:
Векторы скорости и перемещения при равномерном прямолинейном движении направлены в сторону движения тела. 3. Как мы уже сказали, основной задачей механики определение в любой момент времени положения тела, т. е. его координаты. Запишем уравнение зависимости координаты тела от времени при равномерном прямолинейном движении. Это уравнение называют уравнением движения. Пусть тело совершило перемещение sx = х - х0.
С другой стороны, проекция перемещения на ось X равна произведению проекции скорости на эту ось и времени: sx = υxt. Приравнивая правые части выражений, можно записать: х - х0 = υxt. Отсюда координата тела х в любой момент времени t:
Если начальная координата тела х0 = 0, то х = υxt. Таким образом, координату тела при равномерном прямолинейном движении в любой момент времени можно определить, если известны его начальная координата и проекция скорости движения на ось X. Проекции скорости и перемещения могут быть как положительными, так и отрицательными. Проекция скорости положительна, если направление движения совпадает с направлением оси X (см. рис. 8, а). В этом случае х > х0. Проекция скорости отрицательна, если тело движется против направления оси X (рис. 8, б). В этом случае х < х0.
|
|
|



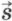 , то скорость его движения
, то скорость его движения 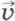 равна
равна