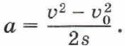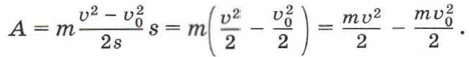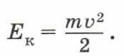|
|
|
|
|
Глава 1. Законы механики § 22. Работа и кинетическая энергияВ каком случае можно говорить, что тело обладает кинетической энергией? От чего зависит кинетическая энергия тела? 1. Предположим, что снаряд, летящий с некоторой скоростью, попадает в доску, пробивает её насквозь и вылетает. Снаряд совершил работу против силы трения, следовательно, он обладал энергией вследствие своего движения. Другой пример. Автомобиль, движущийся с выключенным двигателем, останавливается через некоторое время под действием силы трения. В начале торможения он тоже обладал энергией. Именно за счёт этой энергии автомобиль совершил работу против силы трения.
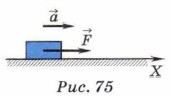
Выясним, от чего зависит кинетическая энергия. 2. Предположим, что на тело массой т действует некоторая сила. Тело при этом перемещается и приобретает ускорение. При перемещении тела сила совершает работу. Будем считать, что сила и перемещение направлены в одну сторону вдоль одной прямой (рис. 75). Если координатная ось X направлена в ту же сторону, то проекции на эту ось силы, перемещения и ускорения движения равны их модулям.
Сила F, действующая на тело, совершает работу А = Fs. Из второго закона Ньютона найдём силу: F = mа. Ускорение, с которым движется тело, равно: Подставив в формулу работы выражения для силы и перемещения, получим:
В левой части равенства стоит работа силы. В правой части равенства стоит разность величин, характеризующих состояние движущегося тела в некоторые моменты времени. Эти величины называют кинетической энергией тела в конечном и начальном положениях. Кинетическая энергия тела вычисляется по формуле:
Следовательно, можно записать А = Ек2 - Eк1, или А = ΔЕк.
|
|
|