|
|
|
|
|
Глава 2. Механические колебания и волны § 24. Математический и пружинный маятникиКакое движение называют колебательным? Какие механические колебательные системы вам известны? 1. Вы уже знаете, что при изучении физических явлений или свойств физических объектов создают их модель. Поступим подобным образом и при изучении колебаний. Существуют системы, представляющие собой тело определённой массы, подвешенное на нити или стержне (например, качели, маятник часов, отвес). Моделью этих систем является математический маятник.
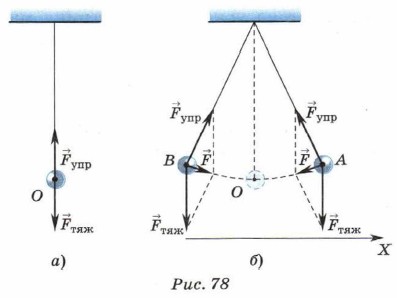
Считается, что нить нерастяжима и не имеет массы, вся масса такого маятника сосредоточена в подвешенном к нити теле. При этом тело можно считать материальной точкой. 2. Рассмотрим процесс колебаний маятника. На маятник действуют равные по модулю и противоположно направленные сила тяжести
Выведем маятник из положения равновесия, отклонив вправо (рис. 78, б). В этом положении (точка А) силы тяжести и упругости будут направлены под углом друг к другу, и их равнодействующая 3. Математический маятник совершает колебания под действием внутренних сил: силы тяжести и силы упругости.
Выясним, как изменяются смещение, скорость и ускорение при движении маятника. Вспомним, что отклонение маятника от положения равновесия называют смещением х, а модуль наибольшего смещения — амплитудой колебаний А. Анализируя процесс колебания маятника, можно сделать вывод, что это движение происходит под действием переменной силы. Это означает, что в процессе движения меняются не только смещение и скорость груза, но и его ускорение. При движении маятника (см. рис. 78) его скорость в крайних положениях А и В равна нулю, а при прохождении через положение равновесия она максимальна. Равнодействующая сил тяжести и упругости максимальна в положениях А и В и равна нулю в положении равновесия. Следовательно, в соответствии со вторым законом Ньютона ускорение маятника максимально в положениях Аи В и равно нулю в положении равновесия.
|
|
|



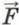 тяж и сила упругости
тяж и сила упругости