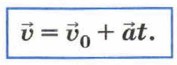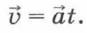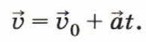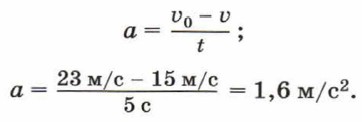|
|
|
|
|
Глава 1. Законы механики Ускорение. Равноускоренное прямолинейное движение4. Преобразовав формулу ускорения при равноускоренном прямолинейном движении, можно получить формулу для нахождения скорости тела в любой момент времени:
Если начальная скорость тела равна нулю, т. е. в начальный момент времени оно покоилось, то эта формула принимает вид:
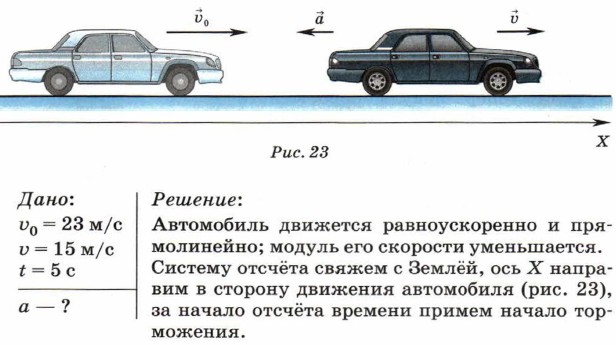
5. При вычислении скорости или ускорения пользуются формулами, в которые входят не векторы, а проекции этих величин на координатную ось. Поскольку проекция суммы векторов равна сумме их проекций, то формула для проекции скорости на ось X имеет вид: υx = υ0x + axt, где υx — проекция скорости в момент времени t, υ0x — проекция начальной скорости, аx — проекция ускорения. При решении задач необходимо учитывать знаки проекций. Так, в случае, изображённом на рисунке 22, а, проекции скоростей и ускорения на ось X положительны; модуль скорости с течением времени возрастает. В случае, изображённом на рисунке 22, б, проекции на ось X скоростей положительны, а проекция ускорения — отрицательна; модуль скорости с течением времени уменьшается. 6. Пример решения задачи Скорость автомобиля при торможении уменьшилась от 23 до 15 м/с. Каково ускорение тела, если торможение длилось 5 с?
Запишем формулу для нахождения скорости при равноускоренном прямолинейном движении:
В проекциях на ось X получим υx = υ0x + axt. Учитывая, что проекция ускорения тела на ось X отрицатель- на, а проекции скоростей на эту ось положительны, запишем: υ = υ0 - at. Отсюда
Ответ: а = 1,6 м/с2.
|
|
|