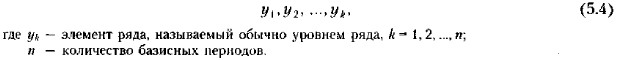5.3.2. Методы обработки временных, пространственных и пространственно-временных совокупностей

Эти методы занимают ведущее место с позиции формализованного прогнозирования и существенно варьируют по сложности используемых алгоритмов. Выбор того или иного метода зависит от множества факторов, в том числе имеющихся в наличии исходных данных. По этому параметру можно выделить три типовые ситуации.

Наличие временного ряда. Эта ситуация встречается на практике наиболее часто: финансовый менеджер или аналитик имеет в своем распоряжении данные о динамике показателя, на основании которых требуется построить приемлемый прогноз.

Динамический (или временной) ряд представляет собой совокупность значений изучаемого показателя, относящихся к некоторым последовательным интервалам или моментам времени; в первом случае ряд называется интервальным, во втором — моментным. Временной интервал, заложенный в основу ряда, чаще всего предполагается постоянным (год, месяц, день и т, п.). Пример интервального ряда: данные о годовом товарообороте магазина за ряд лет; пример моментного ряда: данные о стоимости основных средств данного магазина на начало года за ряд лет.

Динамический ряд обычно представляется следующим образом:

Наиболее типовая ситуация при обработке динамического ряда — выделение тренда. Это можно сделать с помощью различных методов¹:

¹Напомним, что временной ряд характеризуется базовыми количественными характеристиками (темпом роста, темпом прироста, абсолютным значением одного темпа прироста и др.). Подробную информацию об этих характеристиках, равно как и о других инструментальных методах анализа рядов динамики можно найти: (Елисеева, Юзбашев. С. 445—525; Ковалев, 2001(a)].

метод «на глазок». Возможны различные его варианты: например, построение приблизительного графика зависимости по статистическим данным, представленным графически: расчет среднего темпа прироста; определение прогнозируемого значения уровня ряда, главным образом, на основе интуиции и с минимальным привлечением статистических данных. Аналитики шутливо называют подобный способ «методом трех П», от слов: пол, палец, потолок;
метод скользящей средней. Временной ряд делится на сегменты, содержащие, например, по три элемента ряда; для каждой «тройки» рассчитывается средняя. Этим достигается сглаживание отдельных выбросов от общей тенденции. Полученный ряд средних подвергается визуальному или количественному анализу для выявления тенденции;
метод усреднения по левой и правой половинам. Один из вариантов таков: ряд разбивают на две части, находят среднее значение признака для каждой половины, строят график в виде прямой, проходящей через найденные два значения;
метод наименьших квадратов (построение уравнения регрессии, чаще всего линейного, поскольку оно легче поддается интерпретации, хотя возможно построение любой нелинейной формы тренда).

Как пример применения регрессионных моделей для целей прогнозирования упомянем о двух методах: простом динамическом анализе и анализе с помощью авторегрессионных зависимостей. Первый метод исходит из предпосылки, что прогнозируемый показатель (у) изменяется прямо (обратно) пропорционально с течением времени. Поэтому для определения прогнозных значений показателя у строится, например, следующая зависимость;

у_t = а₀ + a_t. (5.5)

где t - порядковый номер периода.

Параметры уравнения регрессии (a₀. a₁) находятся, как правило, методом наименьших квадратов. Подставляя в формулу нужное значение t можно рассчитать требуемый прогноз.

Окончание >>>