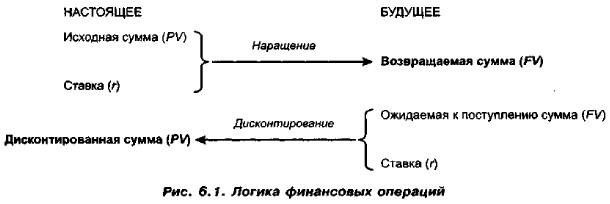
6.2. Операции наращения и дисконтирования (продолжение)

Следует обратить внимание читателя на следующее весьма важное обстоятельство. В формулах (6.1) и (6.2) пока не акцентируется внимание на продолжительности периода, однако из алгоритма расчета с очевидностью следует, что обе ставки являются функцией времени: чем длительнее период, тем существеннее должно быть различие между суммовыми величинами PV и FV, а потому с изменением продолжительности временного интервала, т. е. продолжительности финансовой операции, должна меняться и ставка. Поскольку финансовые операции могут длиться от нескольких дней до нескольких лет, необходимо всегда помнить следующее правило: процентная ставка в финансовой операции должна быть некоторым образом увязана с продолжительностью операции. Обычно это делается путем задания некоторого базисного интервала, к которому привязывается ставка (год, квартал, месяц, день). Чаще всего характеристика финансовой операции делается с помощью годовой процентной ставки.

Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется наращением, искомая величина — наращенной суммой, а используемая в операции ставка — ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется дисконтированием, искомая величина — дисконтированной суммой (иногда используется термин приведенная сумма), а используемая в операции ставка — ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором — о движении от будущего к настоящему (рис. 6.1).

Логика финансовых операций

Итак, в любой простейшей финансовой сделке, предполагающей учет фактора времени с помощью операций наращения и (или) дисконтирования, следующие три параметра являются ключевыми: (а) схема наращения (дисконтирования), (б) используемая ставка, (в) продолжительность базисного периода (т. е. выбранное дробление финансовой операции на базисные периоды); при этом две величины предполагаются заданными, а одна является искомой.

Экономический смысл финансовой операции, задаваемой формулой (6.1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (6.1)

то видно, что время генерирует деньги.

Разность I = (FV - PV ) называется процентом. Это величина дохода от предоставления в долг денежной суммы PV. (Заметим, что в математике процентом называют сотую долю некоторого числа, что, естественно, отличается от экономического понятия «процент».)

На практике доходность является величиной непостоянной, зависящей, главным образом, от степени риска, ассоциируемого с видом бизнеса, в который сделано инвестирование капитала. Связь здесь прямо пропорциональная: чем рискованнее бизнес, тем выше значение доходности. Считается, что наименее рисковы вложения в государственные ценные бумаги или в государственный банк, однако доходность операции в этом случае относительно невысока.

<<< К началу Окончание >>>