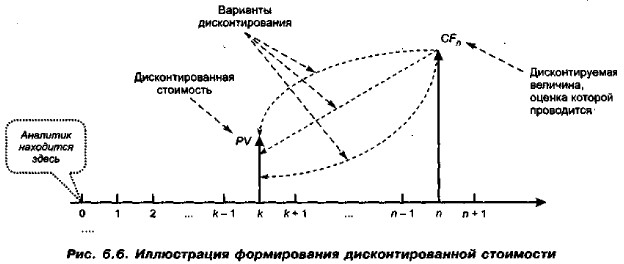
6.4.2. Дисконтированная стоимость единичного платежа

Оценивая целесообразность финансовых вложений в тот или иной вид бизнеса, исходят из того, является ли это вложение более прибыльным (при допустимом уровне риска), чем вложения в государственные ценные бумаги. Используя несложные методы, пытаются проанализировать будущие доходы при минимальном, безопасном уровне доходности.

Основная идея этих методов заключается в оценке будущих поступлений CFn (например, в виде прибыли, процентов, дивидендов) с позиции текущего момента. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылами: (а) происходит перманентное обесценение денег (инфляция); (б) темп изменения цен на сырье, материалы и основные средства, используемые предприятием, может существенно отличаться от темпа инфляции; (в) желательно периодическое начисление (или поступление) дохода, причем в размере не ниже определенного минимума. Базируясь на этих посылах, инвестор должен оценить, какими будут его доходы в будущем, какую максимально возможную сумму допустимо вложить в данное дело исходя из прогнозируемой его рентабельности.

Ключевым в оценке подобных финансовых операций является умение оценки единичного платежа, ожидаемого к получению в будущем. Как уже отмечалось, здесь необходимо учесть фактор времени. В результате появляется понятие дисконтированной стоимости единичного платежа (Present Value of a Single Amount). Этим понятием обозначается оценка суммы, ожидаемой к получению в будущем, с позиции некоторого предшествующего момента времени. При этом предполагается, что промежуток между этими временными моментами разделен на t равных интервалов (рис. 6.6). Чаще всего временные моменты О и n совпадают.

Иллюстрация формировании дисконтированной стоимости

Подчеркнем, что по сути единичный платеж представляет собой частный случай денежного потока {CF_k, k = 12,,.., n}, когда CF_k = 0 при k ≠ n. В инвестиционных расчетах, сопровождающих проекты инвестирования и финансирования, базовой является схема сложных процентов, применяемая и для наращения, и для дисконтирования, а потому расчет дисконтированной стоимости ведется по формуле (6.20), являющейся следствием формулы (6.6).

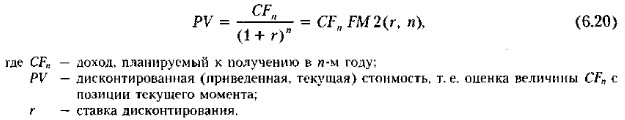
Множитель 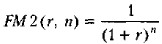называется дисконтирующим множителем для единичного платежа. Как и в случае с множителем FM1(r, n), несложно понять, что значения дисконтирующего множителя не зависят от суммовых величин, а потому их можно табулировать для различных комбинаций {r, n}, что обеспечивает упрощение расчетов на практике (см. Приложение 3). Экономический смысл дисконтирующего множителя FM2(r, n) заключается в следующем. Он показывает сегодняшнюю цену одной денежной единицы будущего, т. е, чему, с позиции текущего момента, равна одна денежная единица (например, один рубль), циркулирующая в сфере бизнеса п периодов спустя от момента, на который осуществляется дисконтирование (обычно он совпадает с моментом расчета), при заданных процентной ставке (доходности) r и частоте начисления процента.

Продолжение >>>