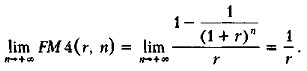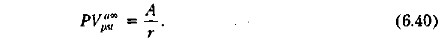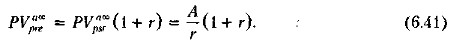|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
Оценка аннуитетов 6.7.2. Оценка бессрочного аннуитетаАннуитет называется бессрочным (Perpetual Annuity), если денежные поступления продолжаются довольно длительное время. Математически это означает, что n → ∞ да. Характерным примером бессрочного аннуитета являются консоли — выпускаемые правительствами некоторых стран облигации, по которым проводят регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 лет и более. Бессрочный аннуитет также называют вечной рентой. В этом случае прямая задача (определение будущей стоимости аннуитета) не имеет смысла, однако обратная задача (определение дисконтированной стоимости аннуитета) имеет решение. Поток платежей в постоянном бессрочном аннуитете при одном денежном поступлении А за период (например, равный году), являющийся базисным для начисления процентов по ставке r, представляет собой бесконечно убывающую геометрическую прогрессию с первым членом
Отсюда следует, что дисконтированная стоимость бессрочного аннуитета постнумерандо находится по формуле
Из формул (6.39) и (6.40) следует, что дисконтированная стоимость бессрочного аннуитета пренумерандо может быть найдена по формуле
Формула (6.40) показывает, что поток даже с неограниченным числом платежей имеет конечную приведенную стоимость. С финансовой точки зрения это понятно, поскольку деньги, которые поступят через много лет, сейчас мало что стоят (а при высокой инфляции практически ничего не стоят). Эта же ситуация проявляется при сравнении коэффициентов дисконтирования бессрочного аннуитета и аннуитетов большой продолжительности. Рассмотрим значения FM4(r, n) при r = 10%.
|
|
|



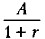 и знаменателем
и знаменателем 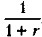 . Для бессрочного аннуитета постнумерандо, используя формулу для определения суммы бесконечно убывающей геометрической прогрессии или переходя в (6.36) к пределу при n → ∞, получим
. Для бессрочного аннуитета постнумерандо, используя формулу для определения суммы бесконечно убывающей геометрической прогрессии или переходя в (6.36) к пределу при n → ∞, получим