|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
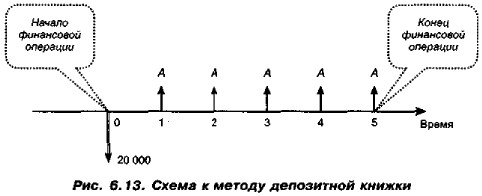
Оценка аннуитетов 6.7.3. Метод депозитной книжкиМожно дать иную интерпретацию расчета дисконтированной стоимости аннуитета с помощью метода депозитной книжки, логика которого такова. Сумма, положенная на депозит, приносит доход в виде процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшается. Как раз эта ситуация имеет место в случае с аннуитетом. Текущая стоимость аннуитета — это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы. Эта сумма годового платежа включает начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение исходного долга осуществляется постепенно, в течение всего срока действия аннуитета. Структура годового платежа постоянно меняется. В начальные периоды в нем преобладают начисленные за очередной период проценты; с течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга. Логику и счетные процедуры метода рассмотрим на примере. Пример В банке получена ссуда на 5 лет в сумме 20 000 долл, под 13% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать надо равными суммами в конце каждого года. Требуется определить величину годового платежа. Решение Если обозначить за А величину искомого годового платежа, то данный финансовый контракт можно представить в виде следующей схемы (рис. 6,13).
Заметим прежде всего, что на рис. 6.13 фактически изображены два денежных потока: первый связан с оттоком денежных средств и состоит из одного элемента, равного величине инвестиции в сумме 20 тыс. долл.; второй связан с притоками денежных средств и представлен аннуитетом постнумерандо (рассуждения приведены с позиции байка). Иными словами, стрелка, де монстр и рующая отток денежных средств, ие является элементом денежного потока, демонстрирующего поступления, т. е. сформулированное выше правило о совпадении числа стрелок и числа базисных интервалов в контексте одного потока здесь выполнено.
|
|
|