|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
Глава 7. Риск и его роль в управлении финансами фирмы 7.1. Сущность риска (продолжение)Таким образом, при оценке рисковости некоторого ожидаемого события нельзя абстрагироваться от величины возможного исхода, а потому при обсуждении этого события в терминах риска надо всегда принимать во внимание обе упомянутые равноважные характеристики — вероятность осуществлен ия исхода и его значимость, т, е. речь должна идти по сути об оценке и субъективной оптимизации комбинации {k, r}, где k — характеристика некоторого исхода (например, величина потери), r — вероятность события с таким исходом. Если оценивать риековость ситуации с вариативным множеством вероятных исходов безотносительно их значимости, то она может быть описана в терминах вариации, т, е. разброса значений исходов, — чем больше разброс, тем более рискова ситуация. С помощью этой характеристики можно делать сравнительную оценку рисковости несколько ситуаций, каждая из которых имеет вариативное множество вероятных исходов (например, имеется несколько ценных бумаг как объектов инвестирования и речь идет о выборе одной из них, причем об ожидаемых доходностях ценных бумаг можно судить лишь в терминах вероятности). В этом случае принятие решения зависит от целевых установок инвестора. Во внимание принимается не только величина разброса вероятных исходов, но и среднее их значение, т, е. вновь можно ориентироваться на комбинацию , где средний исход — некая мера разброса (вариации). Рассмотрим пример. Пример Имеются две лотереи (подбрасывание монеты): (1) лотерея АА обещает выигрыш 100 руб, при выпадении орла и 60 руб. при выпадении решки; (2) лотерея В В обещает выигрыш 70 руб. при выпадении орла и 90 руб. при выпадении решки. Какая из этих лотерей более рискова? Каковы возможные варианты действий игроков? Решение В каждой из лотерей получение того или иного исхода равновероятно Несколько усложним ситуацию. Предположим, что потенциальный игрок нуждается как минимум в сумме 100 руб., меньшая сумма его пи при каких обстоятельствах не устроит. В этом случае он вынужден принимать во внимание не только обособленную рисковость, но и ожидаемое значение исхода. Отсюда с очевидностью следует, что несмотря на повышенный риск, игрок выберет лотерею АА, поскольку другая лотерея его никак не устраивает. Именно эта ситуация (или ее вариации) складывается в большинстве случаев на практике. Предлагаем читателю изменить условия задачи и проанализировать ситуации, когда не совпадают вероятности в лотереях, число возможных исходов и (или) средний выигрыш (проигрыш). Приведенный пример показывает, что оценка ситуации с позиции ее рисково- сти или выбора более или менее рисковой ситуации из нескольких альтернативных многоаспектна. В реальной ситуации число потенциально возможных исходов может быть весьма большим, но осуществится в рамках горизонта планирования лишь один из ыих или близкий к одному из обособленных. Если значения исходов отличаются друг от друга значимо, а вероятности их появления также значимы, то широта вариации значений исходов повышает неуверенность в появлении желаемого исхода. Следовательно, чем больше вариация возможных исходов, тем выше рисковость явления (события). Таким образом, можно сделать следующие выводы. Во-первых, в зависимости от конкретной ситуации, в которой находится лицо, принимающее решения, и поставленной им задачи риск может измеряться по-разному: либо с помощью вероятности (вероятность найти существенный клад на дне моря невысока, а значит, событие, заключающееся в организации экспедиции по поиску клада, является чрезвычайно рисковым), либо с помощью какого-либо показателя вариации возможных исходов (например, чем больше различаются крайние значения возможных исходов некоторой операции, тем более она рискова). Во-вторых, как правило, рисковость оценивается не изолированно, сама по себе, а в связке с ожидаемым (средним) исходом.
|
|
|



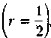 , а потому несложно рассчитать математическое ожидание выигрыша: оно в обеих лотереях равно 80 руб.
, а потому несложно рассчитать математическое ожидание выигрыша: оно в обеих лотереях равно 80 руб. 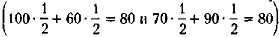 . Таким образом, с позиции значимости среднего исхода лотереи равноценны. Однако с позиции рисковости такой равнозначности уже нет. В лотерее АА разброс ожидаемых исходов выше: размах вариации равен 40 руб. (100 — 60) а в лотерее ВВ — 20 руб. (90 — 70) То есть в лотерее АА можно (в сравнении с лотереей ВВ) более значимо выиграть (возможный максимальный выигрыш в лотерее АА составляет 100 руб., тогда как в лотерее В В — лишь 90 руб.), но можно и более значимо проиграть (при неблагоприятном исходе лотереи АА выигрыш составит 60 руб., тогда как при неблагоприятном исходе лотереи В В выигрыш будет выше и составит 70 руб.). Таким образом, лотерея ВВ менее рискова. Если принимать во внимание только рисковость, то игрок должен отдавать приоритет лотерее ВВ.
. Таким образом, с позиции значимости среднего исхода лотереи равноценны. Однако с позиции рисковости такой равнозначности уже нет. В лотерее АА разброс ожидаемых исходов выше: размах вариации равен 40 руб. (100 — 60) а в лотерее ВВ — 20 руб. (90 — 70) То есть в лотерее АА можно (в сравнении с лотереей ВВ) более значимо выиграть (возможный максимальный выигрыш в лотерее АА составляет 100 руб., тогда как в лотерее В В — лишь 90 руб.), но можно и более значимо проиграть (при неблагоприятном исходе лотереи АА выигрыш составит 60 руб., тогда как при неблагоприятном исходе лотереи В В выигрыш будет выше и составит 70 руб.). Таким образом, лотерея ВВ менее рискова. Если принимать во внимание только рисковость, то игрок должен отдавать приоритет лотерее ВВ.