|
|
|
|
|
Глава 5. Одночлены. Арифметические операции над одночленами § 21. Сложение и вычитание одночленов (окончание)
Выполните действия: 21.27. a) 42b2c3d2 + 54b2c3d4 + 48b2c3d2 + 12b2c3d2;
21.29. a) -1,4a3 - (-0,09a3) + (-1,5a3) + 2a3;
21.32. a) 21xyx2y3x - 8x2y2xyxy - 2xy3x3y - 3x4y3y;
21.34. а) К разности одночленов 16х3у4 и 13х2у4 прибавьте сумму одночленов 23х2у4 и 10х2у4.
21.35. а) Из суммы одночленов 2,38n4р и -1,48n4р вычтите разность одночленов 4,72n4р и -1,28n4р.
21.36. В данном выражении вместо многоточия расставьте знаки «+» и «-» так, чтобы получилось верное равенство: а) 25а2b4 = 3а2b4 ... 5а2b4 ... 7а2b4 ... 10а2b4; б) 43x3у9 = 50х3у9 ... 7х3у9; в) 79c8d10 = 85c8d10 ... 10c8d10 ... 4c8d10; г) 99pnqnzn = 100pnqnzn ... 10pnqnzn ... 15pnqnzn ... 4pnqnzn. 21.37. Некоторое число уменьшили на 15%, а затем результат увеличили на 10 %. После этого получили число, которое на 13 меньше первоначального. Найдите первоначальное число. 21.38. Задуманное число сначала увеличили на 12%, а затем результат уменьшили на 24 %. Полученное при этом число оказалось на 186 меньше задуманного. Найдите задуманное число. 21.39. В прямоугольном параллелепипеде длина в 3 раза больше ширины и в 2 раза меньше высоты. Найдите измерения прямоугольного параллелепипеда, если площадь его поверхности равна 864 см2. 21.40. В прямоугольном параллелепипеде ширина в 2 раза меньше высоты и составляет 21.41. Измерения прямоугольного параллелепипеда относятся как 2 : 3 : 5, а площадь его поверхности равна 62 дм2. Найдите измерения прямоугольного параллелепипеда.
|
|
|



 21.23. Первое число в 1,5 раза больше второго. Известно, что удвоенное первое число на 24 больше, чем третья часть второго. Найдите эти числа.
21.23. Первое число в 1,5 раза больше второго. Известно, что удвоенное первое число на 24 больше, чем третья часть второго. Найдите эти числа.
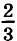 стороны третьего квадрата. Найдите сторону каждого квадрата, если сумма их площадей равна 61 см2.
стороны третьего квадрата. Найдите сторону каждого квадрата, если сумма их площадей равна 61 см2.
 от ребра первого. Найдите ребро каждого куба, если объём первого куба на 296 см3 меньше объёма третьего куба.
от ребра первого. Найдите ребро каждого куба, если объём первого куба на 296 см3 меньше объёма третьего куба.
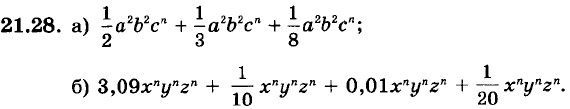
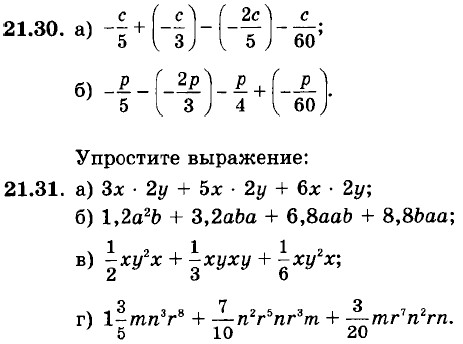
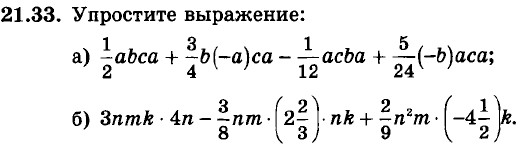
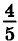 его длины. Найдите измерения параллелепипеда, если площадь его поверхности равна 736 м2.
его длины. Найдите измерения параллелепипеда, если площадь его поверхности равна 736 м2.