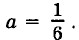|
|
|
|
|
Глава 6. Многочлены. Арифметические операции над многочленами Домашняя контрольная работа № 6 (окончание)Вариант 11. Приведите многочлен к стандартному виду, укажите его степень и свободный член:
2. В выражении 2а2 + 4b - 12 замените переменную 6 многочленом 2а2 - 4а + 1 и приведите получившийся многочлен к стандартному виду. 3. Вместо символа * в многочлене 4. Пусть p1(a) = а2 - 3а3 + 1,2, р2(а) = 3а3 - 2,4а2 - а. Составьте многочлен: а) р(а) = р1(а) + 2р2(а); б) р(а) = 3р1а) - р2(а). 5. При каких значениях переменных верно равенство 6х2у(2ху - 1) + 3х(2ху - 5) = 2х(6х2у2 - 5) - 25? 6. Используя формулу сокращённого умножения, вычислите: а) 992; б) 2022. 7. Решите уравнение (2х - 1)(2х + 1) - 4(х + 5)2 = 19. 8. Используя формулу сокращённого умножения, упростите выражение (2x + 3)(4x2 - 6x + 9) и найдите его значение при х = 0,25. 9. Докажите, что значение выражения (5m - 2)(5m + 2) - (5m - 4)2 - 40m не зависит от значения переменной. Вариант 21. Приведите многочлен к стандартному виду, укажите его степень и свободный член:
2. В выражении 3х3 + 2у + 4 замените переменную у многочленом 3х3 + х - 5 и приведите получившийся многочлен к стандартному виду. 3. Вместо символа * в многочлене 4. Пусть р1(b) = 12b4 - 10b2 + 7, р2(b) = 1,4b3 - 5b4 + b + 1,2. Составьте многочлен: а) р(b) = 2р1(b) + р2(b); б) р(b) = р1(b) - 3р2(b). 5. При каких значениях переменных верно равенство 3а(5аb3 - 3) + 5а2b2(3b - 2а) = 15а(2аb3 - 1) + 18? 6. Используя формулу сокращённого умножения, вычислите: а) 892; б) 1022. 7. Решите уравнение (3х + 2)(3х - 2) - 32 = 9(х - 2)2. 8. Используя формулу сокращённого умножения, упростите выражение (2 - 3а)(4 + 6а + 9а2) и найдите его значение при 9. Докажите, что значение выражения (3b + 2)2 + (7 + 3b)(7 - 3b) - 12b не зависит от значения переменной.
|
|
|



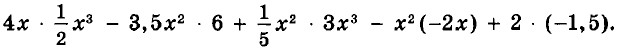
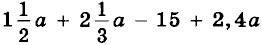 — поставьте такой одночлен, чтобы получившееся выражение не содержало переменной.
— поставьте такой одночлен, чтобы получившееся выражение не содержало переменной.
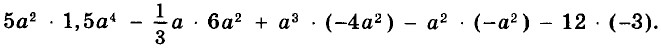
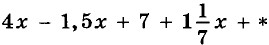 поставьте такой одночлен, чтобы получившееся выражение не содержало переменной.
поставьте такой одночлен, чтобы получившееся выражение не содержало переменной.