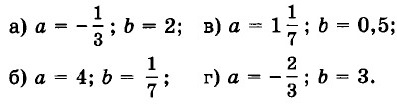§ 32. Способ группировки

32.1. В данных выражениях вынесите общий множитель за скобки. Выпишите попарно те выражения, которые будут содержать одинаковые двучлены:

а) 2x - х², -3аx + 2x², 2аx² - 3а²x, 4ху - 2х²у;
б) ab - 3b², а² - 3аb, 5 + 10x, а + 2аx;
в) n² - nm, 6а² - 9аb, mn - n², 2аb - 3b²;
г) 4х - 8, x² - 2x, -5 - 15m, 21mn + 7n.

32.2. Из данных выражений выпишите попарно те, которые после вынесения общего множителя будут содержать в скобках одинаковые двучлены:

а) 2by - bz, 4ах - az, 2ау - az, 4bx - bz;
б) бах - 3х, -2а + 1, 3by - 3у, с - сb;
в) а³ - 2а², 4ab - 2а2b, 5ас² - 10ас, 3а - 6;
г) 3mn² - 6m²n, abn - 2abm, а²х³ - 9а²х, 6х² - х⁴.

Разложите многочлен на множители:

32.3. a) 3а + 3 + na + n;
6) 6mx - 2m + 9x - 3;
в) ax + 3x + 4a + 12;
г) 2mx - 3m + 4x - 6.

32.4. a) 7kn - 6k - 14n + 12;
6) 7x + 7a - 5ax - 5a²;
в) 9m² - 9mn - 5m + 5n;
г) bc + 3ac - 2ab - 6a².

32.5. a) 5y² + у + y³ + 5;
6) y³ - 4 + 2y - 2y²;
в) z³ + 21 + 3z + 7z²;
г) z - 3z² + z³ - 3.

32.6. a) 7c² - c - c³ + 7;
6) x³ + 28 - 14x² - 2x;
в) x³ - 6 + 2x - 3x²;
г) 2b³ - 6 - 4b² + 3b.

32.7. a) 16ab² + 5b²c + 10c³ + 32ac²;
6) 20n² - 35a - 14an + 50n;
в) 18a² + 27ab + 14ac + 21bc;
г) 2x²yz - 15yz - 3xz² + 10xy².

32.8. Найдите значение выражения:

а) ах - 2а - 3х + 6, если а = 1,5; х = 3,5;
б) 2а + b + 2а² + ab, если а = -1; b = 998;
в) 7by + 4b - 14у - 8, если
г) 5аb -7b + 5а2 - 7а, если а = 3,7; b = -3,7.

Разложите многочлен на множители:

32.9. a) 40a³bc + 21bс - 56ас² - 15а²b²;
б) 16ху² - 5у²z - 10z³ + 32хz²;
в) 30х² + 10с - 25сх - 12x;
г) 18х²z - 10kxy + 20k²y - 36kxz.

32.10. a) ax² - ay - bx² + cy + by - cx²;
б) xy² - by² - ax + ab + y² - a;
в) ax + bx + cx + ay + by + cy;
г) ab - a²b² + a³b³ - c + abc - ca²b².

32.11 Найдите значение выражения 21а²b -4b - 12а + 7аb², если:

Окончание >>>