§ 32. Способ группировки (окончание)

32.12. Решите уравнение:

а) x³ + 2x² + 3x + 6 = 0;
б) x⁴ + x³ - 8x - 8 = 0;
в) x³ + 3х² + 5х + 15 = 0;
г) x4 - 3x³ - x + 3 = 0.

Постройте на координатной плоскости хОу график уравнения:

32.13. а) ху + 2 - 2у - х = 0;
б) 4 + ху + 2(x + у) = 0.

32.14. а) у² - 4у + ху - 4х = 0;
б) 2x² - 4х - ху + 2у = 0;
в) х² + 3х - ху - 3у = 0;
г) -у² + 2у - 3ху + 6х = 0.

Вычислите наиболее рациональным способом:

32.15. а) 2,7 • 6,2 - 9,3 • 1,2 + 6,2 • 9,3 - 1,2 • 2,7;
б) 125 • 48 - 31 • 82 - 31 • 43 + 125 • 83;
в) 14,9 • 1,25 + 0,75 • 1,1 + 14,9 • 0,75 + 1,1 • 1,25;

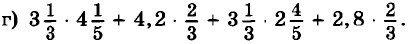
32.16. а) 109 • 9,17 - 5,37 • 72 - 37 9,17 + 1,2 • 72;
б) 19,9 • 18 - 19,9 • 16 + 30,1 • 18 - 30,1 • 16;
в) 15,5 • 20,8 + 15,5 • 9,2 - 3,5 • 20,8 - 3,5 • 9,2;
г) 77,3 • 13 + 8 • 37,3 - 77,3 • 8 - 13 • 37,3.

Разложите многочлен на множители, представив один из его членов в виде суммы подобных слагаемых:

32.17. а) х² + 6x + 8;
б) х² - 8х + 15;
в) х² + 3x + 2;
г) х² - 5х + 6.

32.18. а) а² - 7а + 6;
б) b² + 9b - 10;
в) у² - 10у + 24;
г) z² - 18z - 40.

32.19. а) а² + 8аb - 9b²;
б) а² + 16аb + 55b²;
в) x² + 4ху - 12у²;
г) х² + 16ху + 39у².

Решите уравнение:

32.20. а) x² - 3x + 2 = 0;
б) x² + 8x + 15 = 0;
в) х² - 6x + 8 = 0;
г) х² - 3х - 4 = 0.

32.21. а) 2х² - 5х + 2 = 0;
б) 3x² + 10x + 3 = 0;
в) 4x² + 5x - 6 = 0;
г) 3x² - x - 2 = 0.

32.22. При каком значении р заданная пара чисел является решением уравнения р²х + ру + 8 = 0:

а) (1; -6); б) (-1; 2)?

32.23. При каких значениях р график линейной функции у - р² - 2рх проходит через заданную точку:

а) (1; 3); б) (-2; 5)?

<<< К началу Решенния >>>