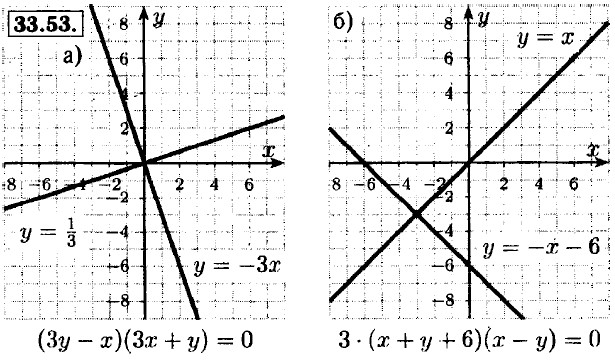
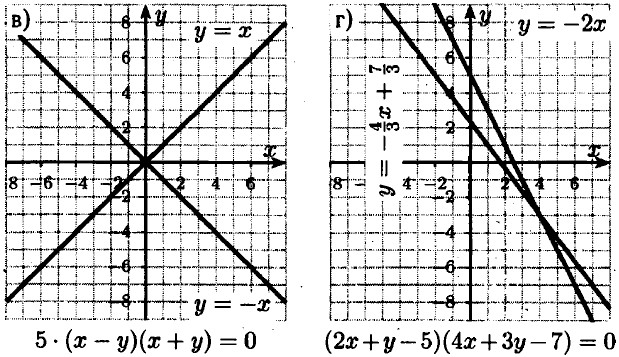
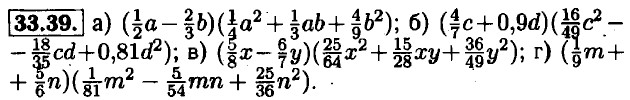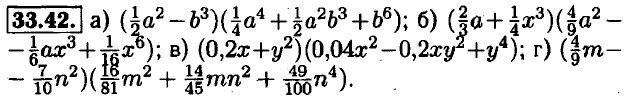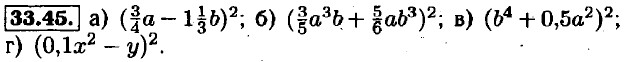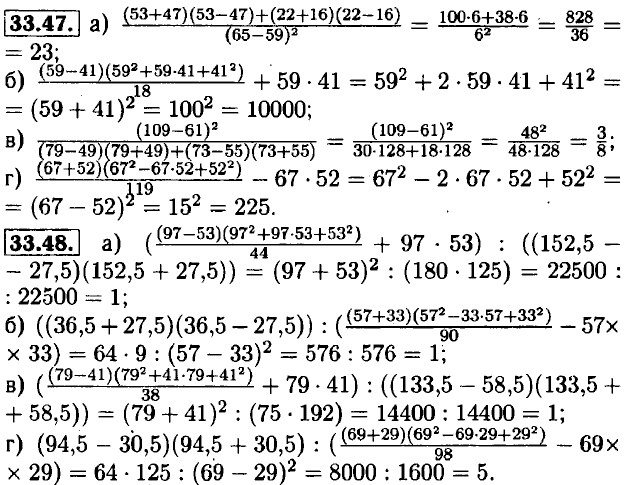Разложение многочленов на множители с помощью формул сокращённого умножения (окончание)

33.40. а) (а² - 2)(а4 + 2а² + 4); б) (0,5 - х²)(0,25 + 0,5х² + x4); в) (3 + b³)(9 - 3b³ + b⁶); г) -(у + 0,25)(у² -0,25у + 0,0625).

33.41. а) (ху - с)(х²у² + хус + c²); б) (m²n + р⁴)(m⁴n² - m²nр⁴ + р⁸); в) (а + mn³)(a² - аmn³ + m²n⁶); г) (у - c⁵d⁶)(q² + qc⁵d⁶ + c¹⁰d¹²).

33.43. a) (2c + 1 - 4)((2c + 1)² + 4 • (2c + 1) + 16) = (2c - 3)(4c² + 12c + 21); 6) (p + 3p - 4)(p² + p(3p - 4) + (3p - 4)²) = (4p - 4)(13p² - 28p + 16); в) (2 - 3 + k)(4 + 2 • (3 - k) + (3 - k)²) = (k - 1)(k² - 8k + 19); г) (5a + 4 - a)((5a + 4)² + a(5a + 4) + a²) = (4a + 4)(31a² + 44a + 16).

33.44. a) (6b + 8 - 5b) ((6b + 8)² + 5b(6b + 8) +25b²) = (b + 8) (91b² + 136b + 64);
б) (10р + 3у - 2p)(100p² - 10p(3y - 2p) + (3p - 2q)²) = (8p + 3y)(84p² - 42py + 9q²);
в) (2x - 5x + 3)(4x² + 2x(5x - 3) + (5x - 3)²) = (3 - 3x)(39x² - 36x + 9);
г) (3x + 2у + 9y)((3x + 2y)² + 9y(3x + 2y) + 81y²) = (3x + 11y)((9x² + 39xy + 103y²).

33.46. a) (51 - 26)(51² + 51 • 26 + 26²) = 25 • (51² + 51 • 26 + 26²);
б) (43 + 17)(43² - 17 • 43 + 17²) = 60 • (43² - 17 • 43 + 17²);
в) (54 - 14)(54² + 14 • 54 + 14²) = 40 • (54² + 14 • 54 + 14²);
г) (38 + 37)(38² - 38 • 37 + 37²) = 75 • (38² - 38 • 37 + 37²).

33.49. а) (а + b)²; б) (6 + 10)²; в) (4a + 7)²; г) (3с - 2)².

33.50. а) (b - 10)²; б) (3р - 7q)²; в) (5а + 0,56)²; г) (0,16 + 10с)².

33.51. а) (4а + 7b)²; б) (15x - 8y)²; в) (8х + 6у)²; г) (10а + 7b)².

33.52. а) (m + 20)²; б) (7р - 5q)²; в) (3а + 7с)²; г) (5z - 8t)².

<<< К началу