Разложение многочленов на множители с помощью комбинации различных приёмов (окончание)

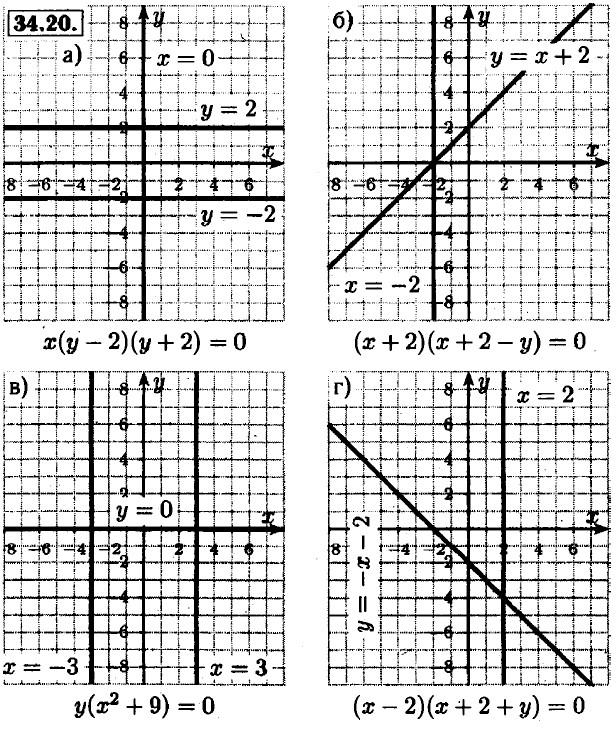
34.21. а) (x - 5)² - 1 = (x - 5 - 1)(x - 5 + 1) = (x - 6)(x - 4); б) (у² - 7)² - 9 = (у² - 7 - 3)(у² - 7 + 3) = (у² - 10)(у² - 4) = (у2 - 10)(у - 2)(у + 2); в) (b² + 2)² - 9 = (b² + 2 - 3)(b² + 2 + 3) = (b² - 1)(b² + 5) = (b - 1)(b + 1)(6² + 5); г) (2а - 3b)² - 4b² = (2а - 3b - 2b)(2а - 3b - 2b) = (2а - b)(2а - 5b).

32.22. a) (2a - 3b)² - 4b² = (2a - 3² - 2²)(2a - 3² - 2²) = (2a - b) (2a - 5b); 6) (3c - 4d)² - 9d² = (3c - 4d - 3d) (3c - 4d - 3d) = (3c - 7d)(3c - d); в) (5a + 2b)² - 16b² = (5a + 2b - 4b)(5a + 2b + 4b) = (5a - 2b)(5a + 6b); г) (3m - 5k)² - 9k² = (3m -5k- 3k)(3m - 5k + Zk) = (3m - 8k)(3m - 2k).

34.23. a) а² + 2а + 5a + 10 - a(a + 2) + 5 • (a + 2) - (a + 5)(a + 2); б) х⁴ + 3x² + 4х² + 12 = х² • (х² + 3) + 4 • (х² + 3) = (х² + 3)(х² + 4); в) b² + b - 4b - 4 = b(b + 1) - 4 • (6 + 1) = (b - 4)(b + 1); г) у⁴ - у² - 4у² + 4 = у2 • (у² - 1) - 4 • (у² - 1) = (у² - 1)(y² - 4) = (у - 1)(y + 1 )(у - 2)(у + 2).

34.24. a) x² + 2xy + 3xy + 6y² = x(x + 2y) + 3y(x + 2y) = (x + 3y)(x + 2y); 6) 4m² - 4mn - mn + n² = = 4m(m - n) - n(m - n) = (4m - n)(m - n); в) p² + pq - 2pq - 2q² = p(p + q) - 2q(p + q) = (p - 2q)(p + q); г) a² + ab + 6ab + 6b² = a(a + b) + 6b(a + b) = (a + 6b)(a + b).

34.25. а) х(х² - 1) = 0; х(х - 1)(х +1) = 0; х = 0; х = 1; х = -1; б) у(16 - у²) = 0; у(4 - у)(4 + у) = 0; у = 0; у = 4; у = -4; в) с² • (с + 1) = 0; с = 0; с = -1; г) d(d² + 1) = 0.

34.26. а) х² • (х + 1) - 4 • (х + 1) = 0; (х² - 4)(х + 1) = 0; (х - 2)(х + 2)(х + 1) = 0; х = 2; х = -2; х = -1 б) у2 • (у + 2) - 4 • (у + 2) = 0; (у² - 4)(у + 2) = 0; (у-2)(у + 2)² = 0; у = 2; у = -2 в) 9 • (z + 1) - z² • (z + 1) = 0; (9 - z²)(z + 1) = 0; (3 - z)(3 + z)(z +1) =0; 2 = 3; z = -3; z = -1 г) р² • (р - 1) - 4 • (р - 1) = 0; (р² - 4)(р - 1) = 0; (р - 2)(р + 2)(р - 1) = 0; р = 2; р = -2; р = 1.

<<< К началу