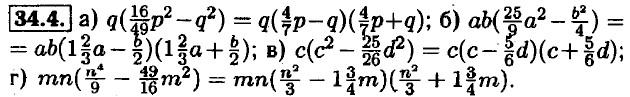|
|
|
|
Главная >> Домашние работы к учебнику Мордкович. Алгебра 7 класс |
|
|
Глава 7. Разложение многочленов на множители Разложение многочленов на множители с помощью комбинации различных приёмов34.1. а) 5х(х2 - 1) = 5х(х - 1)(х + 1); б) 2 • (9b2 - с2) = 2 • (3b - с)(3b + с); в) 3 • (а2 - 4) = 3 • (а - 2)(а + 2); г) 10 • (х2 - у2) = 10 • (х - у)(х + у). 34.2. а) х(х2 - 9) = x(x - 3)(x + 3); б) 3у(у2 - 100) = 3у(у - 10)(у + 10); в) a(64 - а2)a(8 - а)(8 + а); г) 2b(b2 - 144) = 2b(b - 12) (b + 12). 34.3. а) с(с2 - 0,25) = с(с - 0,5)(с + 0,5); б) 2m(25m2 - n2) = 2m(5m - n)(5m + n); в) s(0,04 - a2) - s(0,2 - а)(0,2 + а); г) 3q(16р2 — 25q2) = 3q(4р - 5у)(4р + 5q).
34.5. a) 5 • (а2 + 2аb + b2) = 5 • (а + b)2; б) 2 • (x2 + 2x + 1) = 2 • (x + 1)2; в) 3 • (m2 + n2 — 2mn) = 3 • (m - n)2; г) 8 • (n2 -2n + 1) = 8 • (n - 1)2. 34.6. а) -3 • (x2 - 4x + 4) = -3 • (x - 2)2; б) -2а(а2 - 10аb + 25b2) = -2а(а - 5b)2; в) -5 • (p2 + 2pq + q2) = -5 • (p + q)2; г) -4z(9z2 + 6z + 1) = -4z(3z + 1)2. 34.7. а) (а2 - 4)(а2 + 4) = (а - 2)(а + 2)(а2 + 4); б) (b4 - c4(b4 + с4) = (b2 - с2)(b2 + с2)(b4 + с4) = (b + с)(b - с)(b2 + с2)(b4 + с4); в) (у4 - 1)(у4 + 1) = (у2 - 1)(у2 + 1)(y4 + 1) = (y - 1)(y + 1)(y2 + 1)(y4 + 1); Г) (х2 - z2)(x2 + z2) = (х - z)(x + z)(x2 + z2). 34.8. a) 4 • (m3 - n3) = 4 • (m - n)(m2 + mn + n2); 6) 13 • (а3 + b3) = 13 • (а + b)(а2 - аb + b2); в) 15 • (с3 + d3) = 15 • (c + d)(c2 - cd + d2); г) 21 • (s3 - t3) = 21 • (s - t)(s2 + st + t2). 34.9. a) 6xy(x4 - 4y2) = 6xy(x2 - 2y)(x2 + 2y); б) 0,1xy(x3 - 27y3) = 0,1xу(x - y)(x2 + xy + у2); в) 0,3 • (y2 - 0,81 y6) = 0,3y2 • (1 - 0,9y2)(1 + 0,9y2); г) 3ab2 • (а3 + 8b3) = 3аb2 • (а + 2b)(a2 - 2ab + 4b2). 34.10. a) (m + 3 - 2)((m + 3)2 + 2 • (m + 3) + 4) = (m + 1)(m2 + 8m + 19); 6) (c - 1 + 3)((c - 1)2 - 3 • (c - 1) + 9) = (c + 2)(c2 - 5c + 7); в) (а - 12 - 5)((а - 12)2 + 5 • (а - 12) + 25) = (а - 17)(а2 - 19а + 109); г) (b + 4 + 4)((b + 4)2 - 4 • (b + 4) + 16) = (b + 8)(b2 - 4b + 16). 34.11. a) (х2 + 2х + 1)(x2 - 2х + 1) = (х + 1)2 • (x - 1)2; б) (у2 + 2у - 1 )(у2 + 2у + 1) = (у2 + 2у- 1 )(у + 1)2; в) (9 - с2 - 6с)(9 + с2 + 6с) = (9 - с2 - 6с)(с + 3)2; г) (4m - m + n)(4m + m - n) = (3m + n)(5m - n). 34.12. а) (а + b)2 - с2 = (а + b + с)(а + b - с); б) 1 - (m + n)2 = (1 + m + n)(1 - m - n); в) 16 - (х - у)2 = (4 - x + у)(4 + x - у); г) 4 - (p + q)2 = (2 - p - q)(2 + p + q). 34.13. a) (x - c)2 - d2 = (x - c - d)(x - c + d); 6) (a + 1)2 - b2 = (a + 1 - b)(a + 1 + b); в) (c + 3)2 - d2 = (c + 3 - d)(c + 3 + d); r) r2 - (s + 5)2 = (r - s - 5)(r + s + 5). 34.14. а) (x + у)2 - m2 = (x + у + m)(x + у - m); б) с2 - (а - b)2 = (с - а + b)(с + а - b); в) (m - 4)2 - n2 = (m - 4 - n)(m - 4 + n); г) (q - 3)2 - р2 = (q - 3 - p)(q - 3 + p). 34.15. а) x2 • (x - у) - у2 • (x - у) = (х2 - у2)(х - у) = (x + у)(х - у)2; б) (c - d)(c + d) - 2 • (c + d) = (c - d - 2)(c + d); в) а2 • (а + b) - b2 • (а + b) = (а2 - b2)(a + b) = (а - b)(a + b)2; г) (m - 2n)(m + 2n) - (m + 2n) - (m - 2п - 1)(m + 2n). 34.16. а) (х2 - 2х + 1)(x - 3) = (х - 1)2 • (х - 3); б) (1 - 4а + 4а2)(1 - а)2 = (2а - 1)2 • (а - 1)2. 34.17. а) (а + 2b)(а2 - 2аb + b2) + (а2 - 2аb + b2) = (а + 2b + 1)(а2 - 2аb + b2); б) (2c - d)(4c2 + 2cd + d2) + (4c2 + + 2cd + d2) = (2с - d + 1)(4с2 + 2cd + d2). 34.18. a) (x + 2y)(x2 - 2xy + y ) + (x + 2y)2 = (x + 2y)(x2 - 2xy + y2 + x + 2y); 6) (2p - q)(4p2 + 2pq + q2) + (2p - q)2 = (2p - q)(4p2 + 2pq + q2 + 2p - q). 34.19. a) (a + 2)(a2 - 2a + 4) - a(a + 2) = (a + 2)(a2 - 3a + 4); б) (b + 1)(b2 - b + 1) - 6b(b + 1) = (b + 1)(b2 - 7b + 1). <<< К началу Решенния (окончание) >>>
|
|
|