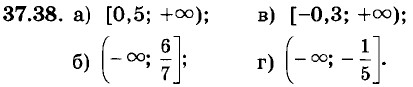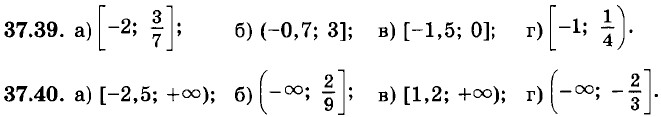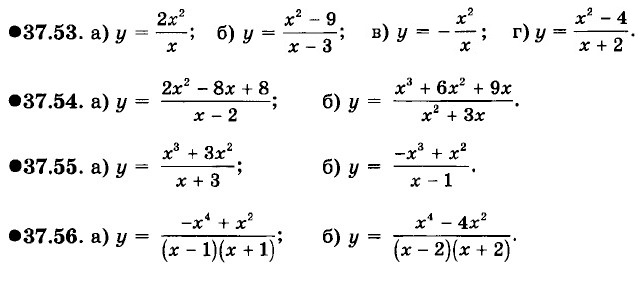|
|
|
|
|
Глава 8. Функция у = х2 § 37. Функция у = х2 и её график (окончание)Найдите наибольшее и наименьшее значения функци у = х2 на заданном отрезке: 37.18. а) [1; 2]; б) [-2; -1]; в) [0; 1]; г) [-3; 0]. 37.19. а) [-1; 1]; б) [-2; 3]; в) [-3; 2]; г) [-1; 3]. 37.20. Не выполняя построения графика, найдите наименьшее значение функции у = х2 на заданном отрезке:
Найдите наибольшее и наименьшее значения функции у = -х2 на заданном отрезке: 37.21. а) [-1; 0]; б) [0; 2]; в) [-2; 0]; г) [2; 3]. 37.22. а) [-2; 2]; б) [-2; 1]; в) [-3; 2]; г) [-1; 3]. 37.23. Не выполняя построения графика, найдите наибольшее значение функции у = -х2 на заданном отрезке:
37.24. Найдите наименьшее значение функции у = х2 на заданном луче: а) [-3; +∞); б) (-∞; -2]; в) (-∞; 1]; г) [1; +∞). 37.25. Найдите наибольшее значение функции у = -х2 на заданном луче: а) (-∞; 0]; б) (-∞; 3]; в) [2; +∞); Г) (-∞; -3].
а) значения функции при значении аргумента, равном -4; 0; 2;
а) значения функции при значении аргумента, равном -3; 0; 1;
Найдите точки пересечения параболы и прямой:
Постройте график функции у = х2 на заданном промежутке: 37.32. а) (1; 3); б) [-2; 2]; в) (0; 2); г) [-2; -1]. 37.33. а) (-∞; 1]; б) [2; +∞); в) (-1; +∞); г) (-∞; 0). 37.34. а) [0; 1); б) (-1; 3]; в) (0; 3]; г) [1; 2). Постройте график функции у = -х2 на заданном промежутке: 37.35. а) [-3; 0]; б) [0; +∞); в) (1; 3); г) (-∞; -1). 37.36. а) (-2; 1); б) (-2; 3]; в) [-1; +∞); г) [-3; 1]. Найдите наибольшее и наименьшее значения функции у = х2 на заданном промежутке: 37.37. а) [-2; 0,5]; б) [-1,5; 0]; в) [-2,5; 1,5]; г) [-3; 2,3].
Найдите наибольшее и наименьшее значения функции у = -х2 на заданном промежутке:
37.41. Пусть А — наименьшее значение функции у = х2 на отрезке [-2; 1], а В — наибольшее значение той же функции на отрезке [-3; -1]. Что больше: А или В? Сделайте графическую иллюстрацию. 37.42. Пусть С — наибольшее значение функции у = х2 на отрезке [1; 2], a D — наименьшее значение функции у = 2х + 3 на отрезке [-1; 1]. Что больше: С или D? Сделайте графическую иллюстрацию. 37.43. Пусть М — наибольшее значение функции у = -х2 на отрезке [-1; 3], а N — наименьшее значение функции у = х на том же отрезке. Что больше: М или N? Сделайте графическую иллюстрацию. 37.44. Пусть L — наименьшее значение функции у = х2 на отрезке [-2; -1], а N — наименьшее значение той же функции на отрезке [1; 2]. Что больше: L или N? Сделайте графическую иллюстрацию. 37.45. Пусть Р — наименьшее значение функции у = х2 на луче (-∞; 3], a Q — наименьшее значение той же функции на луче (-∞; 2]. Что больше: Р или Q? Сделайте графическую иллюстрацию. 37.46. Пусть А — наибольшее значение функции у = х2 на полуинтервале (-1; 2], а В — наименьшее значение функции у = х + 2 на луче [3; +∞). Что больше: А или В? Сделайте графическую иллюстрацию. 37.47. Пусть А — наибольшее значение функции у = х2 на полуинтервале [-3; 2), а B — наименьшее значение функции у = 3x на луче [-1; +∞). Что больше: А или В? 37.48. Пусть R — наименьшее значение функции у = х2 на отрезке [-4; 4], a S — наибольшее значение функции у = -х2 на отрезке [-17; 10]. Не выполняя построения, сравните R и S. 37.49. Найдите точки пересечения параболы и прямой:
37.50. С помощью графика функции у = х2 определите, при каких значениях х выполняется неравенство: а) х2 < 1; б) х2 ≥ 1; в) х2 ≤ 9; г) х2 > 9. 37.51. С помощью графика функции у = -х2 определите, при каких значениях х выполняется неравенство: а) -х2 ≤ -4; б) -х2 > -9; в) -х2 ≥ -4; г) -х2 < -9. 37.52. С помощью графика функции у = х2 определите, при каких значениях х выполняется неравенство: а) 1 < х2 < 4; б) 4 ≤ х2 ≤ 9. Постройте график функции:
|
|
|



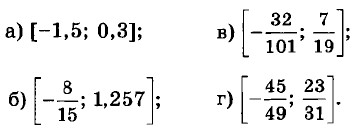
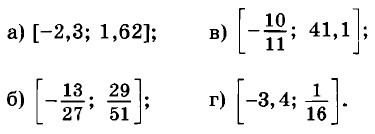
 37.26. Постройте график функции у = х2. С помощью графика найдите:
37.26. Постройте график функции у = х2. С помощью графика найдите: