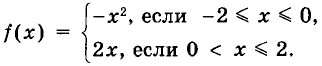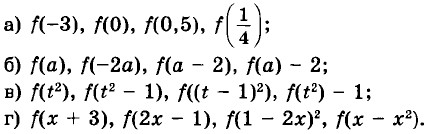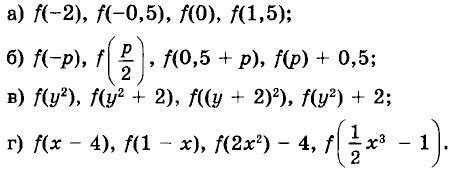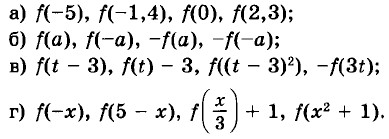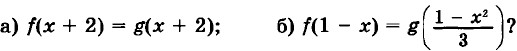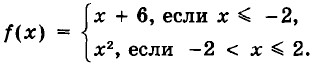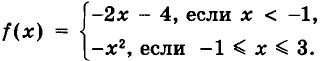|
|
|
|
|
Глава 9. Итоговое повторение Функции и графики (окончание)26. При каких значениях а, b, с график уравнения ах + by + с = 0: а) проходит через начало координат;
27. Постройте график функции у = х2. С помощью графика определите: а) значения функции, если значение аргумента равно -1; 0,5; 2,5;
28. Постройте график функции у = -х2. С помощью графика определите: а) значения функции, если значение аргумента равно -3; 1,5; 2;
29. Постройте график функции у = х2. С помощью графика определите: а) значения функции, если х ≥ 1;
30. Постройте график функции у = -х2. С помощью графика определите: а) значения функции, если х < -2;
31. Найдите наибольшее и наименьшее значения функции у = х2:
32. Найдите наибольшее и наименьшее значения функции У = -х2: а) на отрезке [-2; 1];
Решите графически уравнение: 33. а) х2 = 9; б) -х2 = 2х; в) х2 = -3х; г) -х2 = 2. 34.
35. Решите графически неравенство:
36. Постройте график функции у = ƒ(x), где
С помощью графика найдите: а) ƒ(-1), ƒ(1), ƒ(2);
37. Постройте график функции у = ƒ(x), где
С помощью графика найдите: а) ƒ(-1), ƒ(0), ƒ(2);
38. Постройте график функции у = ƒ(x), где
С помощью графика найдите: а) область определения функции;
39. Дана функция у = ƒ(x), где ƒ(x) = 4х - 1. Найдите:
40. Дана функция у = ƒ(x), где ƒ(x) = 2x + 3. Найдите:
41. Дана функция у = ƒ(x), где ƒ(x) = x2. Найдите:
42. Дана функция у = ƒ(x), где ƒ(x) = -х2. Найдите: а) ƒ(-8), ƒ(-1,7), ƒ(1), ƒ(2,1);
43. а) Даны функции у = ƒ(x) и у = g(x), где ƒ(x) = 2х - 5,
g(x) = -3x + 4. При каком значении х выполняется равенство ƒ(x - 1) = g(x + 1)?
44. Дана функция у = ƒ(x), где ƒ(x) = х2. При каком значении х выполняется равенство: а) ƒ(х + 1) = ƒ(x - 2);
45. Даны функции у = ƒ(x) и у = g(x), где ƒ(x) = -x2, g(x) = 3х- 10. При каких значениях х выполняется равенство:
46. Дана функция у = ƒ(x), где
Построив график функции у = ƒ(x), определите, при каких значениях р уравнение ƒ(x) = р:
47. Дана функция у = ƒ(x), где
Построив график функции у = ƒ(x), определите, при каких значениях р уравнение ƒ(x) = р:
|
|
|