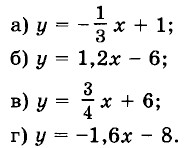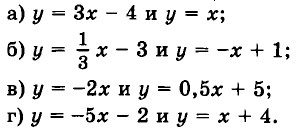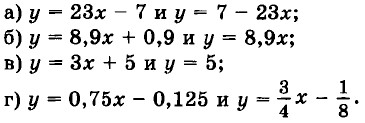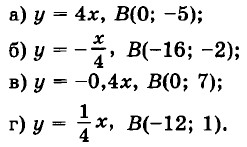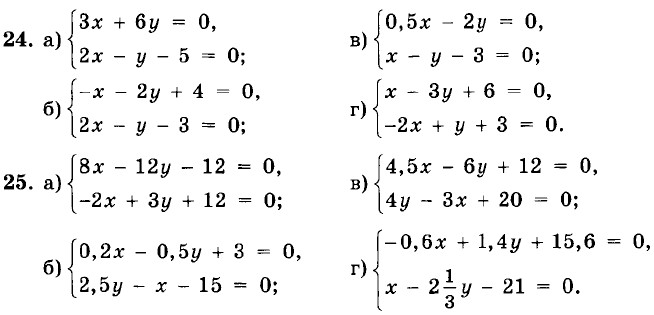|
|
|
|
|
Глава 9. Итоговое повторение Функции и графики1. а) Отметьте на координатной плоскости точку Р(-1; 2).
Найдите точку, симметричную данной относительно оси ординат.
2. а) Изобразите на координатной плоскости точку А(-3; 3) и прямую х = -2. Найдите точку, симметричную данной относительно построенной прямой,
3. а) Даны точки А(-1; 4) и В(-1; 8). Найдите прямую, которая
является осью симметрии для этих двух точек. Отметьте точку С(-2; 5) и найдите точку, симметричную ей относительно найденной прямой. Укажите ещё одну пару симметричных точек.
4. а) Даны точки С(2; 4) и D(1; 5). Постройте прямую, симметричную
прямой СО относительно оси абсцисс,
5. Функция задана формулой у = kx + m. Назовите значения коэффициентов k, m и охарактеризуйте график заданной функции, если:
6. Не выполняя построения графика функции, укажите координаты точки пересечения прямой с осью у:
7. Не выполняя построения графика, определите, возрастает или убывает данная функция:
Изобразите схематично график функции у = kx + m согласно следующему условию: 8.
9.
10. Постройте график функции у = х - 6. По графику найдите: а) значение функции, если значение аргумента равно -2; 0; 3;
11. Постройте график функции у = -х + 1. По графику найдите: а) значение функции, если значение аргумента равно -3; 0; 2;
12. Постройте график функции у = 2х - 2. С помощью графика найдите: а) координаты точек пересечения прямой с осью х и осью у;
13. Постройте график функции у = -0,5x + 2. С помощью графика найдите: а) координаты точек пересечения прямой с осью х и осью у,
14. Найдите координаты точек пересечения прямой с осью х и осью у:
15. Определите, принадлежит ли графику данной линейной функции точка А, если: а) у = 0,6x + 30, А(-25; 15);
16. Найдите наименьшее и наибольшее значения линейной функции: а) у = -3x на отрезке [-2; 1];
17. Найдите точку пересечения прямых графическим и аналитическим методами:
18. Задайте формулой функцию у = kx, график которой проходит через точку:
19. Определите взаимное расположение графиков функций, если:
20. Задайте линейную функцию, график которой параллелен графику функции у = kx и проходит через точку В, если:
Постройте график заданной функции. 21. Постройте график функции у = 3х + 6. С помощью графика решите неравенство:
22. Используя графический метод, решите неравенство:
23. Постройте график уравнения:
Решите графически систему уравнений:
|
|
|