§ 6. Координатная плоскость (окончание)

6.29. Постройте прямую, симметричную прямой АВ:

а) относительно оси х, если А(4; 1), В(-1; -4);
б) относительно оси у, если А(0; 3), В(-3; 0);
в) относительно оси х, если А(-2; 0), В(0; 6);
г) относительно оси у, если А(-6; -3), В(4; 2).

6.30. Постройте:

а) ΔАВС, если А(6; 0), В(2; -3), С(3; 2);
б) ΔA₁B₁C₁, симметричный ΔАВС относительно оси х;
в) ΔА₂В₂С₂, симметричный ΔАВС относительно оси у;
г) ΔА₃В₃С₃, симметричный ΔАВС относительно начала координат.

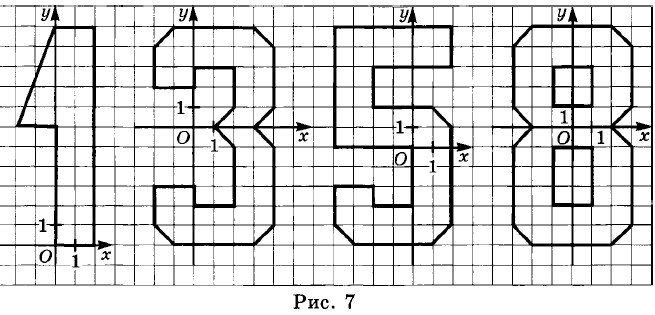
6.31. Даны три вершины А(1; 1), В(1; 3), С(3; 3) квадрата ABCD. Найдите координаты точки D, постройте этот квадрат и ещё три квадрата, один из которых расположен ниже данного на пять единиц, второй — на две единицы правее данного, третий — на три единицы ниже и пять единиц левее данного. Назовите координаты вершин третьего квадрата А₃В₃С₃D₃.

6.32. Запишите координаты точек, с помощью которых можно построить цифры, изображённые на рис. 7:

а) цифра 1; б) цифра 3; в) цифра 5; г) цифра 8.

6.33. Найдите координаты вершин С и D квадрата ABCD, если известны координаты вершин А(3; 1) и В(3; -4). Сколько решений имеет задача?

6.34. Известны координаты двух противоположных вершин квадрата ABCD: А(2; -2) и С(-2; 2). Найдите координаты двух других вершин. Сколько решений имеет задача?

6.35. Длина стороны квадрата ABCD равна 6, а координаты вершины А равны (-2; 3). Найдите координаты остальных вершин, зная, что сторона АВ квадрата параллельна оси ординат и что начало координат лежит внутри квадрата.

6.36. Квадрат со стороной 8 расположен так, что центр его находится в начале координат, а стороны параллельны осям координат. Определите координаты вершин квадрата.

На координатной плоскости постройте точки по заданным координатам и последовательно соедините их отрезками. Какая фигура при этом получится?

6.37. а) Д-1; 5), 2(-3; 5), 3(-3; 9), 4(-2; 10), 5(3; 10), 6(3; 4), 7(0; 1), 8(3; 1), 9(3; -1), 10(-3; -1), 11(-3; 1), 12(1; 5), 13(1; 8), 14(-1; 8);

б) 1(0; 7), 2(-1; 0), 3(0; 0), 4(0; 2), 5(2; 2), 6(2; 0), 7(3; 0), 8(3; -2), 9(2; -2), 10(2; -4), 11(0; -4), 12(0; -2), 13(-3; -2), 14(-3; 0), 15(-2; 7).

6.38. а) 1(4; 2), 2(4; 4), 3(3; 5), 4(-1; 5), 5(-2; 4), 6(-2; -5), 7(-1; -6), 8(3; -6), 9(4; -5), 10(4; -1), 11(3; 0), 12(0; 0), 13(0; 3), 14(2; 3), 15(2; 2), 16(2; -2), 17(2; -4), 18(0; -4), 19(0; -2);

б) 1(-1; 3), 2(-3; 3), 3(-3; 5), 4(-2; 6), 5(2; 6), 6(3; 5), 7(3; 2), 5(-1; -5), 9(-3; -5), 10(1; 2), 11(1; 4), 12(-1; 4).

6.39. а) 1(8; 2), 2(11; 2), 3(8; 9), 4(4; 10), 5(2; 9), 6(-1; 13), 7(-8; 10), 8(-9; 9), 9(-8; 7), 10(-12; 7), 11(-И; 10), 12(-15; 12), 13(-19; 11), 14(-15; 9), 15(-14; 3), 16(-7; 5), 17(-5; -3), 15(-6; -6), 19(-2; -6), 20(-3; -4), 21 (-3; 3), 22(4; 3), 23(5; -3), 24(3; -5), 25(3; -6), 26(7; -6), 27(6; -5), 25(8; 7);

б) 1(0; -7), 2(3; 2), 3(6; 2), 4(7; 5), 5(7; 10), 6(6; 16), 7(9; 16), 5(5; 18), 9(2; 11), 10(1; 13), 11(-9; 11), 12(-10; 11), 13(-9; 7), 14(-8; 7), 15(-9; 5), 16(-4; 1), 17(-2; 2), 15(-2; -10), 19(4; -10).

6.40. a) 1(-3; 5), 2(-3; 3), 3(-1; 3,5), 4(-2,5; 2), 5(-8,5; 2), 6(-1; 0), 7(0; 0), 3(-3; -4), 9(-1; -6,5), 10(-2,5; -7), 11(0; -7), 12(-1; -3), 73(1; -2,5), 14(3; -2,5), 15(3; -3), 16(7; -3), 17(8; -5), 13(8; -3), 19(4; -1), 20(0; 2), 21(0; 3), 22(4; 3,5), 23(0; 4,5), 24(-1; 3,5);

б) 1(5; 5,5), 2(2,5; 8,5), 3(1; 8), 4(0,5; 5), 5(1,5; 3,5), 6(0,5; 4), 7(-2; 3,5), S(-4,5; 1), 9(-5; 0,5), 10(-5,5; -5), 11 (-3,5; -1,5), 12(-4; -3,5), 13(-2,5, -2), 14(-2; -3,5), 15(—2,5; -3,5), 16(-0,5; -8,5), 17(-1; -10), 13(1,5; -10), 10(-0,5; -8,5), 20(-0,5; -0,5), 21(3; 2,5), 22(2; 5,5), 23(2,5; 6,5).

<<< К началу Решенния >>>