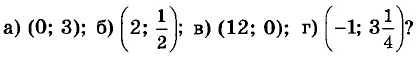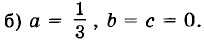|
|
|
|
|
Глава 2. Линейная функция § 7. Линейное уравнение с двумя переменными и его график (окончание)
а) x - у = -1 и 2x + у = 4;
Дано линейное уравнение с двумя переменными. Используя его, выразите каждую из переменных через другую:
7.25. Среди решений уравнения х + Зу - 20 = 0 найдите такую пару, которая состоит: а) из двух одинаковых чисел;
7.26. Найдите значение коэффициента а в уравнении ах + 5y - 40 = 0, если известно, что решением уравнения является пара чисел: а) (3; 2); б) (9; -1); 7.27. Найдите значение коэффициента b в уравнении 6х + by - 35 = 0, если известно, что решением уравнения является пара чисел: а) (0; 1); б) (3; 8,5); 7.28. Найдите значение коэффициента с в уравнении 8x + 3у - с = 0, если известно, что решением уравнения является пара чисел: а) (2; -1); 7.29. При каком значении т решением уравнения mх + 4у - 12m = 0 является пара чисел:
Решите задачу, использовав для составления математической модели две переменные и построив затем графики соответствующих линейных уравнений: 7.30. Сумма двух чисел равна 5, а разность равна 1. Найдите эти числа. 7.31. Сумма двух чисел равна 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в сумме эти числа дадут 8. Найдите исходные числа. 7.32. Разность двух чисел равна 1. Если первое число оставить без изменения, а второе увеличить в 3 раза, то в сумме эти числа дадут 9. Найдите исходные числа. 7.33. Разность двух чисел равна 3. Найдите эти числа, если известно, что уменьшаемое больше вычитаемого в 4 раза. 7.34. В шахматном турнире участвовало 10 учеников. Мальчиков было в 1,5 раза больше, чем девочек. Сколько мальчиков и сколько девочек участвовало в турнире? 7.35. На дополнительные занятия по математике девочек пришло в 3 раза больше, чем мальчиков. Сколько всего учеников пришло на дополнительные занятия, если мальчиков оказалось на 6 человек меньше, чем девочек? Постройте на координатной плоскости прямую, заданную уравнением ах + by + с = 0, при следующих значениях коэффициентов а, b и с: 7.36. а) а = 2, b = 1, с = -3;
7.37. а) а = 0, b = 2, с = -6;
7.38. а) а = с = 0, b = 0,2; 7.39. При каких значениях коэффициентов а, Ь, с прямая ах + by + с = 0: а) параллельна оси x;
|
|
|



 7.21. Найдите координаты точки пересечения прямых:
7.21. Найдите координаты точки пересечения прямых:
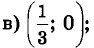 г) (-2; 2,4).
г) (-2; 2,4).
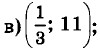 г) (-5; -13).
г) (-5; -13).
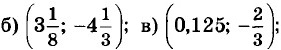 г) (0; 0).
г) (0; 0).