Линейное уравнение с двумя переменными и его график (окончание)

7.25. a) x + 3y - 20 = 0; x = 20 - 3y.
Для того чтобы пара чисел состояла из двух одинаковых чисел, нужно чтобы х = у : х = 20 - 3х; х = 5; у = х = 5.
Ответ: (5; 5)
б) Пусть х = 2у, тогда уравнение примет вид 2у + 3у - 20 = 0.
5у = 20; у = 4; х = 2у = 2 • 4 = 8.
Ответ: (8; 4).

7.27. а) b - 35 = 0; b = 35; б) 18 + 8,5у - 35 = 0; 8,5b = 17; b = 2; в) 2 + 11b - 35; 11b = 33; b = 3; г) -30 - 13b - 35 = 0; 13b = -65; b = -5.

7.28. а) 16 - 3 - с = 0; с = 13; б) 25 - 13 - с = 0; с = 12;
в) 1 - 2 - с = 0; с = -1; г) -с = 0. с = 0.

7.29. а) 12 - 2m = 0; m = 6; б) 2m + 2 - 12m = 0; -10m = -2; m = 0,2; в) 12m - 12m = 0; 0 = 0; При любом m; г) -m + 13 - 12m = 0; 13m = 13; m = 1.

7.30. Пусть х — первое число.
Тогда (5 - х) — второе число.
x - (5 - x) = 1; х - b + х = 1; х = 3 — первое число;
5 - 3 = 2 — второе число.
Ответ: 3; 2

7.31. Пусть х — первое число.
Тогда (7 - х) — второе число.
2x + 7 - х = 8; х = 1 — первое число; 7 - 1 = 6 — второе число.
Ответ: 1; 6.

7.32. Пусть х — первое число.
Тогда (х - 1) — второе число. х + 3 • (х - 1) = 9; 4х - 12; х = 3 — первое число; 3 - 1 = 2 — второе число.
Ответ: 3; 2.

7.33. Пусть х — вычитаемое.
Тогда 4х — уменьшаемое.
4х - х = 3; х = 1 — вычитаемое; 4 • 1 = 4 — уменьшаемое.
Ответ: 1; 4.

17.34. Пусть x — девочек участвовало в турнире.
Тогда 1,5x — мальчиков участвовало в турнире.
1,5x + х = 10; х = 4 — девочек участвовало в турнире.
1,5 • 4 = б — мальчиков участвовало в турнире.
Ответ: 4; 6.

7.35. Пусть х — пришло мальчиков.
Тогда 3x — пришло девочек.
3x - x = 6; x = 3 — пришло мальчиков.
3 • 3 = 9 — пришло девочек.
Ответ: 3; 9.

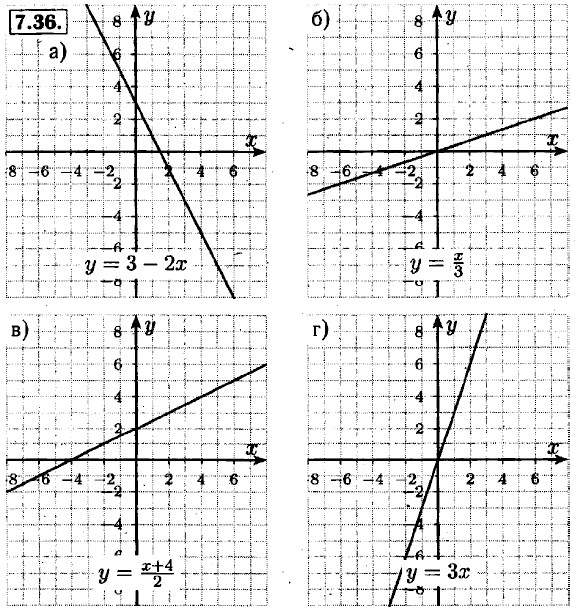
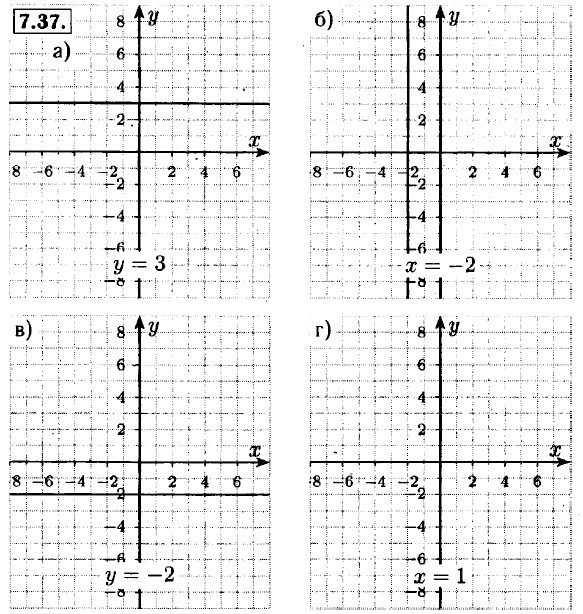
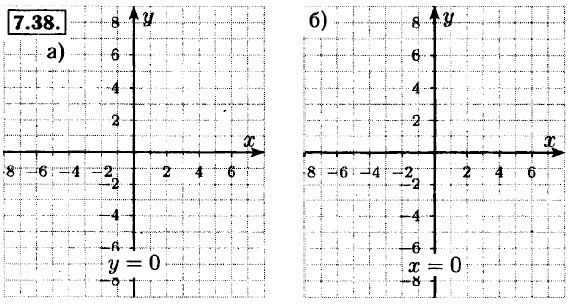
7.39. а) а = 0, b ≠ 0, с ≠ 0; б) а ≠ 0, b = 0, с ≠ 0; в) а ≠ = 0, b ≠ 0, с = 0; г) а = 0, b ≠ 0, с = 0; а ≠ 0, b = 0, с = 0.

<<< К началу