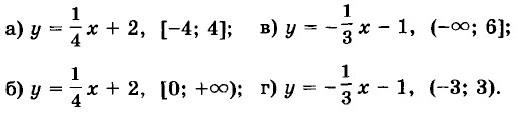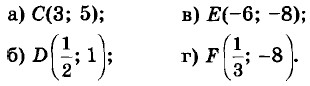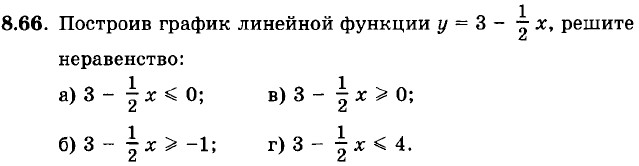§ 8. Линейная функция и её график (окончание)

8.48. Постройте график линейной функции у = -2x + 6 и с его помощью найдите:

а) координаты точки пересечения графика с осью абсцисс;
б) все значения аргумента, при которых выполняется неравенство у > 0;
в) решение неравенства -2х + 6 < 0;
г) значения х, при которых выполняется неравенство у > 6.

8.49. Постройте график линейной функции у = х + 5 и с его помощью найдите:

а) координаты точек пересечения графика с осями координат;
б) все значения аргумента, при которых выполняется неравенство у < 0;
в) отрезок оси х, на котором выполняется неравенство 0 < у < 5;
г) наименьшее и наибольшее значения линейной функции на отрезке [-4; 1].

8.50. Постройте график линейной функции у = -3x + 6 и с его помощью найдите:

а) координаты точек пересечения графика с осями координат;
б) отрезок оси х, на котором выполняется неравенство -3 ≤ у ≤ 0;
в) все значения аргумента, при которых выполняется неравенство у > 0;
г) наименьшее и наибольшее значения линейной функции на отрезке [-1; 2].

8.51. Найдите координаты точек пересечения с осями координат графика линейной функции:

а) у = 7,5x + 45;
б) у = 2,6x - 7,8;

в) у = 3,4x - 27,2;
г) у = 18,1х + 36,2.

8.52. Выясните, проходит ли график линейной функции у = 3,2x - 5 через точку:

а) А(3; 4,6);
б) B(1,2; 0);

в) С(7,5; 4);
г) D(2,2; 2,04).

8.53. Найдите наименьшее и наибольшее значения линейной функции на заданном промежутке:

а) у = 0,5x + 3, [2; 3);
б) у = -0,5x + 1, [-2;+∞);

в) у = 2,5x - 4, (1; 2];
г) у = 2,5x - 4, (-∞; 0].

8.54. Найдите наименьшее и наибольшее значения линейной функции на заданном промежутке:

8.55. а) Найдите точку графика линейной функции у = 3х - 12, абсцисса которой равна ординате.
б) Найдите точку графика линейной функции у = 5х + 4, абсцисса которой равна ординате.

8.56. а) Найдите точку графика линейной функции у = 2х + 9, абсцисса и ордината которой — противоположные числа.
б) Найдите точку графика линейной функции у = -3x + 8, абсцисса и ордината которой — противоположные числа.

8.57. а) Найдите точку графика линейной функции у = х + 15, абсцисса которой в 2 раза меньше ординаты. б) Найдите точку графика линейной функции у = 2х - 35, абсцисса которой в 3 раза больше ординаты.

8.58. Найдите значение т, если известно, что график линейной функции у = -5х + m проходит через точку:

а) N(1; 2);
б) K(0,5; 4);

в) N(-7; 8);
г) Р(1,2; -3).

8.59. Найдите значение k, если известно, что график линейной функции у = kx + 4 проходит через точку:

8.60. Пусть А — наибольшее значение линейной функции у = 2х - 3 на отрезке [0; 2], а B — наибольшее значение линейной функции у = 0,5x - 4 на том же отрезке. Что больше: А или В? Сделайте графическую иллюстрацию.

8.61. Пусть С — наименьшее значение линейной функции у = х - 4 на луче [0; +∞), a D — наименьшее значение линейной функции у = 4 - х на луче (-∞; 1]. Что больше: С или D? Сделайте графическую иллюстрацию.

8.62. Определите знаки коэффициентов k и m, если известно, что график линейной функции у = kx + m проходит:

а) через первый, второй и третий координатные углы плоскости хОу;
б) через первый, второй и четвёртый координатные углы плоскости хОу;
в) через первый, третий и четвёртый координатные углы плоскости хОу;
г) через второй, третий и четвёртый координатные углы плоскости хОу.

8.63. Как расположен в координатной плоскости хОу график линейной функции у = kx + m, если известно, что:

а) k > 0, m = 0;
б) k < 0, m = 0;

в) k = 0, m ≠ 0;
г) k = 0, m = 0?

8.64. Составьте уравнение прямой, проходящей через точку пересечения графиков линейных функций у = 9х - 28 и у = 13х + 12 параллельно:

а) оси абсцисс; б) оси ординат.

8.65. Построив график линейной функции у = 2х + 4, решите неравенство:

а) 2х + 4 > 0;
б) 2х + 4 < 4;

в) 2х + 4 < 0;
г) 2х + 4 > 2.

<<< К началу Решенния >>>