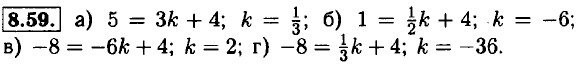|
|
Глава 2. Линейная функция



Линейная функция и её график (окончание)
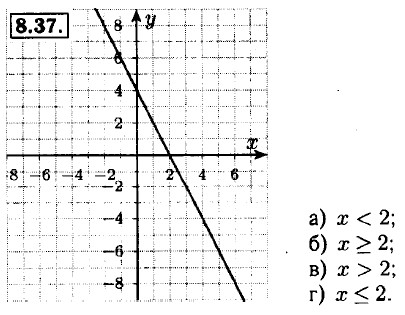
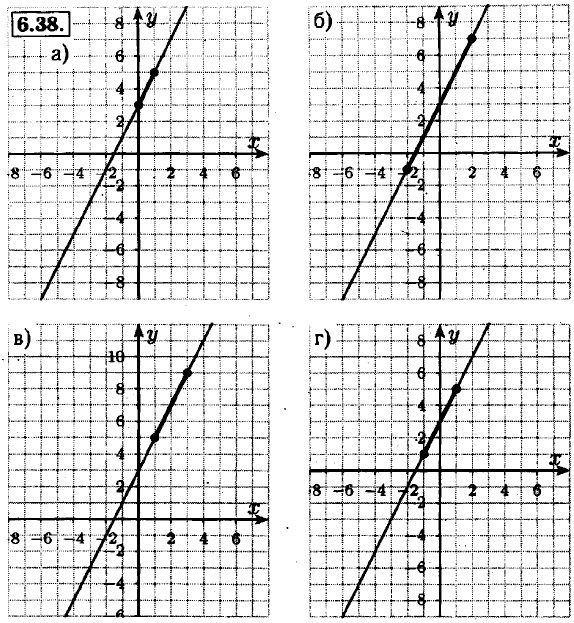
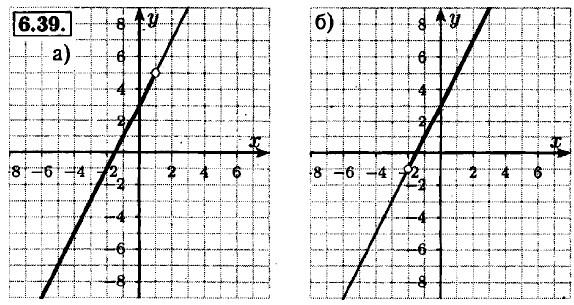
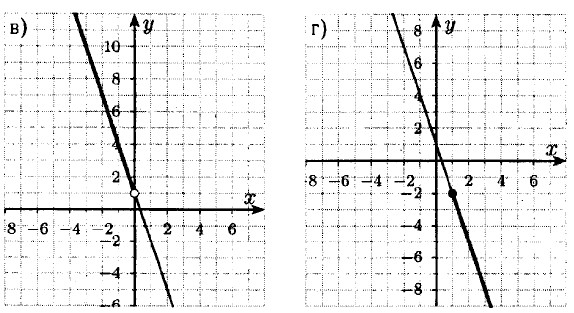
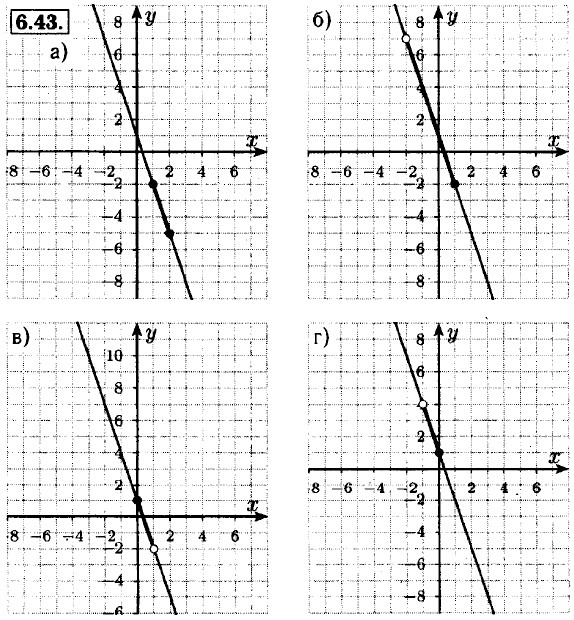
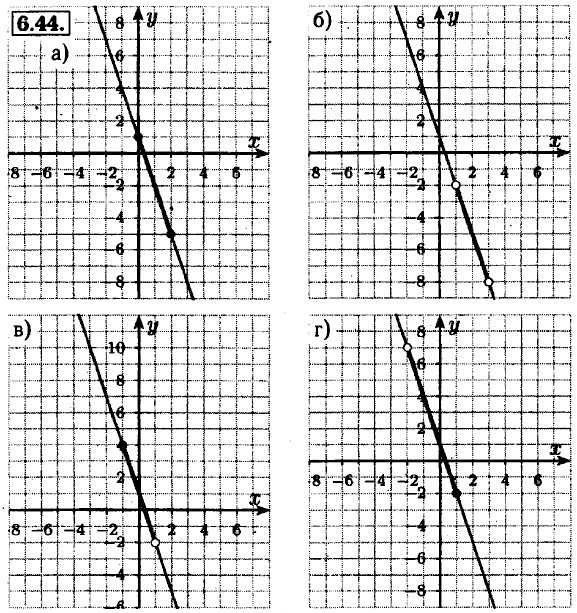
8.45. а) -2 + 3 = 1, -1 + 3 = 2; 1 — наименьшее; 2 — наибольшее; б) -(-1) + 5 = 6, -4 + 5 = 1; 1 — наименьшее; 6 — наибольшее; в) -3 + 3 = 0, -1 + 3 = = 2; 0 — наименьшее; 2 — наибольшее; г) -2 + 5 = 3, -5 + 5 = 0; 0 — наименьшее; 3 — наибольшее.
8.46. а) 4 • (-1) - 1 = -5, 4 • 2 - 1 = 7. -5 — наименьшее; 7 — наибольшее; б) -20 + 5 = 5, -2 • 4 + 5 = -3. -3 — наименьшее; 5 — наибольшее; в) 3 • (-1) - 2 = -5, 3 • 1 - 2 = 1. -5 — наименьшее; 1 — наибольшее; г) -5 • 0 + 7 = 7, -5 • 2 + 7 = -3. -3 — наименьшее; 7 — наибольшее.
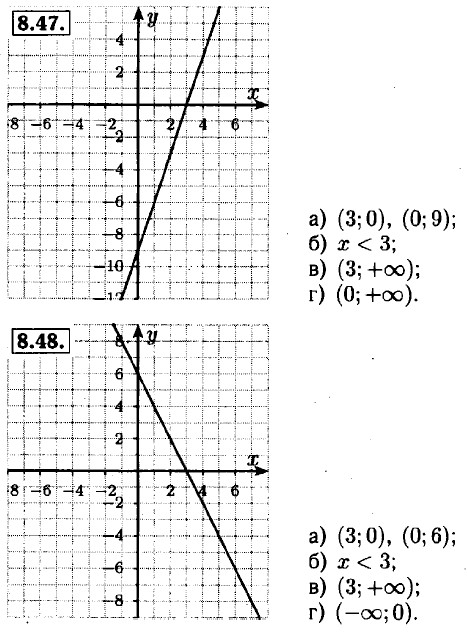
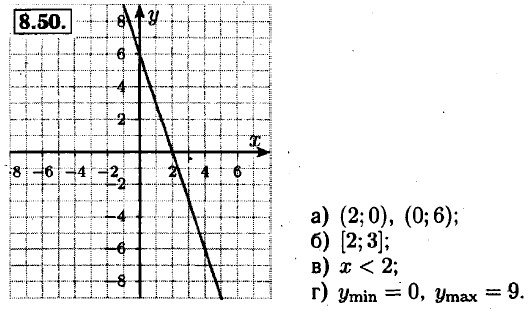
8.51. а) у = 7,5x + 45 ⇒ 7,5x + 45 = 0 ⇒ у = 7,5 • 0 + 45 ⇒ x = -6; у = 45 ⇒ (-6; 0), (0; 45);
б) у = 2,6x - 7,8 ⇒ 2,6x - 7,8 = 0 ⇒ у = 2,6 • 0 - 7,8 ⇒ х = 3; у = -7,8 ⇒ (3;0), (0; -7,8);
в) у = 3,4x - 27,2 ⇒ 3,4x - 27,2 = 0 ⇒ у = 3,4 • 0 - 27,2 ⇒ х = 8; у = -27,2 ⇒ (8; 0), (0; -27,2);
г) у = 18,1x + 36,2 ⇒ 18,1x + 36,2 = 0 ⇒ у = 18,1 • 0 + 36,2 ⇒ x = 3; у = 36,2 ⇒ (3; 0), (0; 36,2).
8.52. а) 3,2 • 3 - 5 = 4,6 - верно; б) 3,2 • 1,2 - 5 = 0 — неверно; в) 3,2 • 7,5 - 5 = 4 — неверно; г) 3,2 • 2,2 - 5 = 2,04 — верно.
8.53. а) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наибольшее равно 0,5 • 2 + 3 = 4. Наименьшего нет.
б) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наименьшего значения не существует. Наибольшее равно -0,5 • (-2) + 1 = 2.
в) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наибольшее равно 2,5 • 1 - 4 = -1,5, 2,5 • 2 - 4 = 1.
г) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в начале промежутка стоит знак -∞, следовательно, наименьшего значения не существует. Наибольшее равно 2,5 • 0 - 4 = -4.
8.54. а) Наибольшее равно 0,25 • 4 + 2 = 3; Наименьшее равно 0,25 • -4 + 2 = 1.
б) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наибольшего значения не существует. Наименьшее равно 0,25 • 0 + 2 = 2.
в) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в начале промежутка стоит знак -∞, следовательно, наибольшего значения не существует. Наименьшее равно 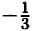 • 6 - 1 = -3. • 6 - 1 = -3.
г) Заданный промежуток является интервалом, следовательно, наибольшего и наименьшего значений не существует.
8.55. а) x = 3x -12; 2x = 12; х = 6. (6; 6); б) х = 5x + 4; 4х = -4; х = -1. (-1; -1).
18.56. а) -х = 2х + 9; 3х = -9; x = -3. (-3; 3); б) -x = -3x + 8; 2x = 8; x = 4. (4; -4).
18.57. а) 2x = x + 15; x = 15; у = 2 • 15 = 30. (15; 30); б) у = 6у - 35; у = 7; x = 3 • 7 = 21. (21; 7).
8.58. а) -5 • 1 + m = 2; m = 7; б) -5 • 0,5 + m = 4; m = 6,5; в) -5 • (-7) + m = 8; m = -27; г) -5 • 1,2 + m = -3. m = 3.
8.62. а) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т. е. k > 0. Но еще известно, что функция проходит через второй координатный угол. Откуда следует, что m > 0.
б) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т. е. k < 0. Но еще известно, что функция проходит через первый координатный угол. Откуда следует, что m > 0.
в) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т. е. k > 0. Но еще известно, что функция проходит через четвертый координатный угол. Откуда следует, что m < 0.
г) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т. е. k < 0. Но еще известно, что функция проходит через третий координатный угол. Откуда следует, что m < 0.
8.63. а) Первый, третий; б) Второй, четвертый, в) Первый, второй, г) Прямая Ох.
8.64. 9х - 28 = 13х + 12 ⇒ х = -10; у = -118. а) у = -118; б) х = -10.
<<< К началу
|














 • 6 - 1 = -3.
• 6 - 1 = -3.