|
|
|
|
|
Глава 2. Функции Вычисление значений функции по формулеФункции, которые мы рассматривали в предыдущем пункте, задавались различными способами. Наиболее распространённым способом является задание функции с помощью формулы. Формула позволяет для любого значения аргумента находить соответствующее значение функции путём вычислений. Пример 1. Пусть функция задана формулой
Найдём значения у, соответствующие целым значениям х:
Результаты вычислений удобно записать в виде таблицы, поместив в верхней строке значения аргумента, а в нижней строке соответствующие значения функции:
Мы выбирали каждый раз значение х на 1 больше предыдущего. Говорят, что мы составили таблицу значений функции с шагом 1. В рассмотренном примере была указана область определения функции. Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл. Например, область определения функции, заданной формулой у = х(х + 5), состоит из всех чисел, а область определения функции, заданной формулой С помощью формулы, задающей функцию, решают также задачу отыскания значений аргумента, которым соответствует данное значение функции. Пример 2. Функция задана формулой у = 12х - 3,6. Найдём, при каком значении х значение функции равно 2,4.
2,4 = 12х - 3,6. Решив его, найдём, что х = 0,5. Значит, у = 2,4 при х = 0,5. Заметим, что мы смогли решить эту задачу, так как она свелась к уравнению, способ решения которого нам известен.
ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646-1716) — немецкий философ, математик, физик и языковед. Он и английский учёный И. Ньютон создали (независимо друг от друга) основы важного раздела математики — математического анализа. Лейбниц ввёл многие понятия и символы, употребляемые в математике и сейчас, в частности им введён термин «функция».
|
|
|



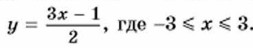
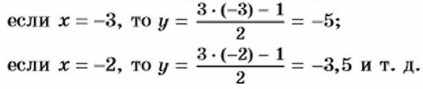

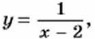 состоит из всех чисел, кроме числа 2.
состоит из всех чисел, кроме числа 2.
 Подставим в формулу у = 12х - 3,6 вместо у число 2,4. Получим уравнение с переменной х:
Подставим в формулу у = 12х - 3,6 вместо у число 2,4. Получим уравнение с переменной х:

