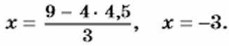Способ подстановки

Рассмотрим способ решения систем линейных уравнений с двумя переменными, называемый способом подстановки. Начнём с примера.

Пример 1. Решим систему уравнений

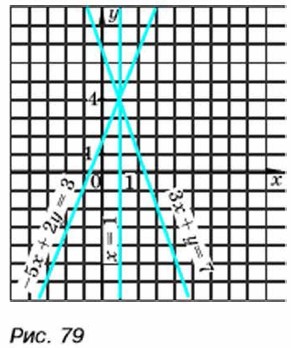
Выразим из первого уравнения у через х: у = 7 - 3х. Подставив во второе уравнение вместо у выражение 7 - 3х, нолучим систему

Нетрудно показать, что системы (1) и (2) имеют одни и те же решения.

В системе (2) второе уравнение содержит только одну переменную. Решим это уравнение:

-5х + 14 - 6х = 3,

-11х = -11,

х = 1.

Подставив в равенство у = 7 - 3х вместо х число 1, найдём соответствующее значение y:

y = 7 - 3 • 1,

у = 4.

Пара (1; 4) — решение системы (2), а значит, и системы (1).

Решение системы (1) мы свели к решению системы (2). При этом мы воспользовались тем, что системы (1) и (2) имеют одни и те же решения.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений системы (1) пересекаются в той же точке, что и графики уравнений системы (2), т. е. все три прямые пересекаются в одной точке (рис. 79).

Мы решили систему (1), используя способ подстановки. При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой по ременной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример 2. Решим систему уравнений

Выразим из второго уравнения х через у: 3х = 9 - 4р,

Подставим в первое уравнение вместо буквы х выражение

Решим полученное уравнение с переменной у:

7(9 - 4у) + 3 • 6р = 3 • 6,

63 - 28у + 18у= 18,

-10y = -45, у = 4,5.

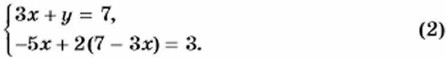
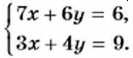
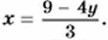
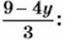
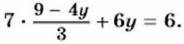
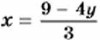Подставим в уравнение вместо у число 4,5:

Ответ, х = -3, у = 4,5.

Окончание >>>