|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
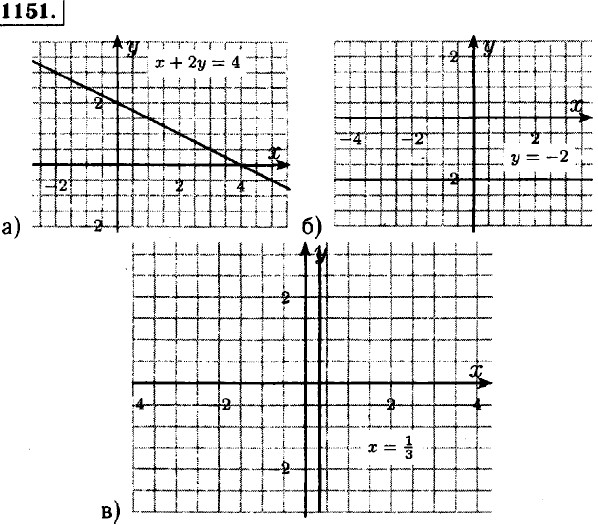
Решенния упражнений Дополнительные упражнения к параграфу 151137. а) нет; б) нет; в) да; г) да. 1138. a) u + υ = 13; б) u + 2υ = -14; в) 10u + 5υ = 2; г) 5u - 10υ = 29. 1139. Дано: ах + by = 81, (15; 40); 15а + 40b = 81 ⇒ 3а + 8b = 16,2; а и 6 не могут быть целыми. 1140. а) х = 5, у = 7; решение уравнения ах = 2у = 1; 5а = 14 = 1; а = 3; б) х = =3, у = 8; решение уравнения 5х + by = 17; -15 + 8b = 17; 8b = 32; b = 4. 1141. а) х + у = 11; решением уравнения являются пары чисел (1; 10), (2; 9), (3; 8), (4; 7), (5; 6), (6; 5), (7; 4), (8; 3), (9; 2), (10; 1). б) ху = 18; решением уравнения являются пары чисел (1; 18). (2; 9); (3; 6); (6;3), (9; 2), (18; 1). 1142. а + b = 42; выпишем простые числа до 41: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41. Очевидно, что решением являются пары чисел (5; 37), (11; 31), (13; 29), (19; 23), (23; 19), (29; 13), (31; 11), (37; 5). 1143. Пусть первоначальное число 1144. Пусть 1145. Пусть 1146. Чтобы график уравнения у - х2 = 9 пересекал: а) ось х необходимо чтобы у = 0 в этой точке. -х2 = = 9 — не имеет решения, значит график не пересекает ось x. б) ось у необходимо чтобы х = 0 в этой точке, у = 9, значит у - х2 = 9 пересекает ось у в точке (0; 9). 1147. х - ху = 46: у = -1,3 ⇒ х • (1 + 1,3) = 46 ⇒ х = 20. Ответ: абсцисса этой точки равна 20. 1148. 8х - 5у = 14: х = 1,2 ⇒ 9,6 - 5у = 14 ⇒ у = -0,88. Ответ: ордината этой точки -0,88. 1149. Дано: 3х + 2у = -4. Предположим что х > 0 и у > 0 тогда, 3х > 0 и 2у > 0 и 3х + 2у > 0 но -4 < 0. Значит графику данного уравнения не принадлежит ни одна точка, у которой обе координаты положительны. 1150. Если ж и у целочисленные, тогда х - 2у также являются целочисленными. Но, 6x - 12у = 5 ⇒ х - 2у =
<<< К началу Решенния (окончание) >>>
|
|
|



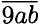 , тогда
, тогда 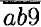 + 576 ⇒ 900 + 10а + b = 100а + 10b + 9 + 576 ⇒ 90а + 9b = 315; на разряд единиц влияет только переменная b, и так как b принимает значения только от 0 до 9; то 5 единственное подходящее число, 90а + 45 = 315 ⇒ а = 3. Ответ: 935.
+ 576 ⇒ 900 + 10а + b = 100а + 10b + 9 + 576 ⇒ 90а + 9b = 315; на разряд единиц влияет только переменная b, и так как b принимает значения только от 0 до 9; то 5 единственное подходящее число, 90а + 45 = 315 ⇒ а = 3. Ответ: 935.
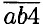 данное число, тогда
данное число, тогда 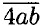 + 7 = 2 •
+ 7 = 2 • 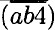 ⇒ 400 + 10а + b + 7 = 200а + 20b + 8. На разряд единиц влияет только переменная b, значит b + 7 = 8; b = 1, 400 + 10а + 8 = 200а + 20 + 8 ⇒ 190а = 380 ⇒ а = 2. Ответ: 214.
⇒ 400 + 10а + b + 7 = 200а + 20b + 8. На разряд единиц влияет только переменная b, значит b + 7 = 8; b = 1, 400 + 10а + 8 = 200а + 20 + 8 ⇒ 190а = 380 ⇒ а = 2. Ответ: 214.
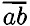 искомое двухзначное число, значит 1аb1 = 21 •
искомое двухзначное число, значит 1аb1 = 21 • 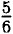 — противоречие, значит x и у не могут быть одновременно целочисленными.
— противоречие, значит x и у не могут быть одновременно целочисленными.