§ 11. Основные понятия (окончание)

В примерах 1 и 2 мы применили графический метод решения системы линейных уравнений. Этим же методом мы пользовались в § 7 при решении задачи о числе яблонь у двух садоводов (система (2) решена в § 7 графическим методом).

К сожалению, графический метод, как и «метод угадывания», не самый надёжный: например, прямые могут пересечься в точке, координаты которой по чертежу не очень легко определить.

Пример 3. Решить систему уравнений:

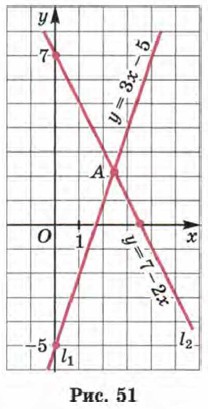
Р е ш е н и е. Построим графики уравнений системы. Здесь есть смысл преобразовать оба уравнения к виду линейной функции. Из первого уравнения получаем у = 3х - 5, а из второго у = 7 - 2х.

Построим в одной системе координат графики линейных функций у = 3х - 5 (прямая (х на рис. 51) и y = 7 - 2х (прямая 12 на рис. 51). Они пересекаются в точке А, координаты которой — единственное решение заданной системы. А вот чему конкретно равны абсцисса и ордината точки А, мы по рисунку 51 точно определить не сможем (точка А как бы «висит» внутри определённой клеточки). Придётся нам позднее вернуться к этому примеру (см. с. 72—73).

Но всё-таки графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы:

графиками обоих уравнений системы (1) являются прямые; эти прямые могут пересекаться, причём только в одной точке, — это значит, что система (1) имеет единственное решение (так было в рассмотренных в этом параграфе системах (2), (4), (5));

эти прямые могут быть параллельны — это значит, что система не имеет решений (говорят также, что система несовместна — такой была система (3));

эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (говорят также, что система неопределённа).

Итак, мы познакомились с новой математической моделью — системой двух линейных уравнений с двумя переменными. Наша задача — научиться её решать. «Метод угадывания» ненадёжен, графический метод также выручает не всегда. Значит, нам нужно располагать надёжными алгебраическими методами решения системы двух линейных уравнений с двумя переменными. Об этом и пойдёт речь в следующих параграфах.

Вопросы для самопроверки

1. Подберите три решения уравнения х + 2у - 9 = 0.

2. Что такое система двух линейных уравнений с двумя переменными?

3. Что называют решением системы двух линейных уравнений с двумя переменными?

4. Придумайте систему двух линейных уравнений с двумя переменными, которая имеет своим решением пару:

а) (0; -1); б) (3; 0); в) (1; 2).

5. Придумайте систему двух линейных уравнений, которая не имеет решений.

6. Расскажите, как графически решить систему двух линейных уравнений с двумя переменными, которая составлена вами в задании 4 в).

7. Что такое неопределённая система уравнений?

8. Что такое несовместная система уравнений?

<<< К началу