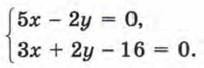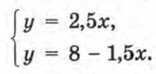§ 12. Метод подстановки

Вернёмся ещё раз к системе (2) из § 11:

Мы её решили графическим методом в § 7 и знаем, что х = 2,у = 5 — единственное решение этой системы. А теперь решим ту же систему другим способом.

Первое уравнение преобразуем к виду 2у = 5х, т. е. у = 2,5x. Второе уравнение преобразуем к виду 2у = 16 - 3х и, далее, у = 8 - 1,5x (все коэффициенты уравнения 2у = 16 - 3х разделили на 2). Теперь систему можно переписать так:

Ясно, что нас интересует такое значение х, при котором 2,5х = 8 - 1,5х. Из этого уравнения находим:

2,5х + 1,5х = 8;

4х = 8;

х = 2.

Если х = 2, то из уравнения у = 2,5х получим у = 5. Итак, (2; 5) — решение системы (что, напомним, нам уже было известно).

Чем эти рассуждения отличаются от тех, что мы применяли в § 7? Тем, что никаких графиков строить не пришлось, вся работа шла на алгебраическом языке. Как же мы рассуждали?

Мы выразили у через х из первого уравнения и получили у = 2,5х. Затем подставили выражение 2,5х вместо у во второе уравнение и получили 2,5х = 8 - 1,5х. Далее решили это уравнение относительно х и получили х = 2. Наконец, по формуле у = 2,5х нашли соответствующее значение у. И вот что важно: во втором уравнении совсем не обязательно было выражать у через х, можно было подставить 2,5х вместо у в заданное уравнение 3х + 2у - 16 = 0. Смотрите:

Зх + 2 • 2,5х -16 = 0;

3х + 5х = 16;

8х = 16;

х = 2.

Подобный метод рассуждений называют обычно методом подстановки. Он представляет собой определённую последовательность шагов, т. е. некоторый алгоритм.

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки
1. Выразить у через х из первого уравнения системы.
2. Подставить полученное на первом шаге выражение вместо у во второе уравнение системы.
3. Решить полученное на втором шаге уравнение относительно х.
4. Подставить найденное на третьем шаге значение х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пары значений (х; у), которые были найдены соответственно на третьем и четвёртом шагах.

Замечание. У вас не возник вопрос, почему у выражают именно из первого уравнения и подставляют во второе, почему не выразить у из второго уравнения и не подставить в первое? И вообще, почему выражали у через х, а не х через у, почему такое неравноправие? Ответ: никакой причины нет. Выражайте, что хотите, но ищите наиболее простые варианты.

Окончание >>>