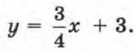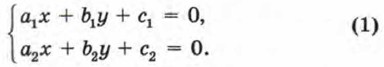|
|
|
|
|
Глава 3. Системы двух линейных уравнений с двумя переменными § 11. Основные понятияВ § 7 мы ввели понятие линейного уравнения с двумя переменными — так называют равенство ах + by + с = 0, где а, b, с — конкретные числа, а х, у — переменные. Примеры линейных уравнений с двумя переменными: 2х - 3у + 1 = 0; х + у - 3 = 0; s - 5t + 4 = 0 (здесь переменные обозначены по-другому: s, t, но это роли не играет). В том же § 7 мы ввели понятие решения линейного уравнения с двумя переменными — так называют всякую пару чисел (х; у), которая удовлетворяет уравнению, т. е. обращает равенство с переменными ах + by + с = 0 в верное числовое равенство. На первом месте всегда пишут значение переменной х, на втором — значение переменной у. Приведём примеры. 1. (2; 3) — решение уравнения 5х + 3у - 19 = 0. В самом деле, 5 • 2 + 3 • 3 - 19 = 0 — верное числовое равенство. 2. (-4; 2) — решение уравнения 3х - у + 14 = 0. Действительно, 3 • (-4) - 2 + 14 = 0 — верное числовое равенство. 3. 4. (1; 2) не является решением уравнения 2х - 3у + 1 = 0. В самом деле, 2 • 1 - 3 • 2 + 1= 0 — неверное числовое равенство (получается, что -3 = 0). В § 8 мы отмечали, что математическую модель ах + by + с = 0 при b ≠ 0 можно заменить более простой у = kx + m. Например, уравнение 3x - 4у + 12 = 0 можно преобразовать к виду
Графиком линейного уравнения ах + by + с = 0, если хотя бы один из коэффициентов а, b отличен от нуля (случай а = 0, b = 0 мы в этой главе рассматривать не будем), является прямая (см. § 7). Координаты любой точки этой прямой удовлетворяют уравнению ах + by + с = 0, т. е. являются решением уравнения. Сколько же решений имеет уравнение ах + by + с = 0? Столько же, сколько точек расположено на прямой, служащей графиком уравнения ах + by + с = 0, т. е. бесконечно много. Многие реальные ситуации при переводе на математический язык оформляются в виде математической модели, состоящей из двух линейных уравнений с двумя переменными. С такой ситуацией мы встретились в § 7 в задаче про двух садоводов Иванова и Петрова. Математическая модель состояла из двух уравнений: 5х - 2у = 0 и 3x + 2у - 16 = 0, причём нас интересовала такая пара значений (x; у), которая одновременно удовлетворяла и тому и другому уравнению. В таких случаях обычно не говорят, что математическая модель состоит из двух уравнений, а говорят, что математическая модель представляет собой систему уравнений. Вообще если даны два линейных уравнения с двумя переменными х и у: ах1 + b1у + с1 = 0 и а2х + b2у + с2 = 0 — и поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют и тому и другому уравнению, то говорят, что заданные уравнения образуют систему уравнений. Уравнения системы записывают друг под другом и объединяют специальным символом — фигурной скобкой:
|
|
|



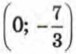 — решение уравнения -0,4x + 3у + 7 = 0. Имеем
— решение уравнения -0,4x + 3у + 7 = 0. Имеем 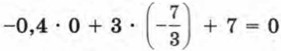 — верное числовое равенство.
— верное числовое равенство.