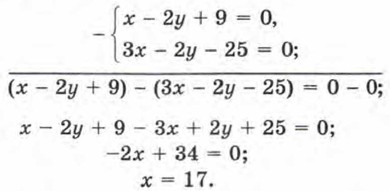§ 14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (окончание)

В чисто учебных целях решим эту систему двумя способами.

Первый способ. Применим метод подстановки. Из первого уравнения системы находим х = 2у - 9. Подставим этот результат вместо х во второе уравнение системы. Получим

3(2у - 9) - 2у - 25 = 0;

4у = 52;

y = 13.

Так как х = 2у - 9, то х = 2 • 13 - 9 = 17.

Итак, х = 17, у = 13 — решение системы.

Второй способ. Применим метод алгебраического сложения:

Подставим найденное значение х в первое уравнение системы, т. е. в уравнение х - 2у + 9 = 0:

17 - 2у + 9 = 0;

y = 13.

Итак, х = 17, у - 13 — решение системы.

Второй этап мы завершили (решили полученную систему, причём даже двумя способами).

Третий этап. Ответ на вопрос задачи.

Спрашивается, сколько школьников было в седьмом классе на уроках в среду, когда пришли все ученики. Поскольку х = 17, у = 13, т. е. в классе было 17 девочек и 13 мальчиков, делаем вывод: всего в классе 17 + 13 = 30 учеников.

О т в е т: 30 школьников.

Замечание. Вы, конечно, понимаете, что для решения конкретной системы уравнений надо выбирать тот способ, который представляется для данного случая наиболее уместным, или тот, который вам больше нравится (т.е. вы можете использовать графический метод, метод подстановки или метод алгебраического сложения — это ваше дело). Составленную в рассмотренной задаче систему мы решили двумя способами, чтобы повторить методы подстановки и алгебраического сложения и сопоставить эти методы друг с другом.

Вопросы для самопроверки

1. Придумайте задачу, математической моделью которой является система двух линейных уравнений с двумя переменными. Составьте соответствующую математическую модель.

2. Решите систему уравнений, полученную вами в п. 1, методом подстановки и методом алгебраического сложения. Сравните получившиеся у вас ответы при решении системы уравнений.

<<< К началу