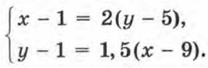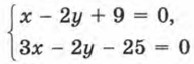§ 14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций

Собственно говоря, ничего особенно нового вы в этом параграфе не узнаете. Ведь вам уже известно, что реальная ситуация может быть описана на математическом языке в виде математической модели, представляющей собой систему двух линейных уравнений с двумя переменными. Так было в § 7 в ситуации с садоводами Ивановым и Петровым. Так было и в примере 2 из § 11. Поэтому теоретический разговор, соответствующий названию параграфа, можно считать законченным. А вот с практической точки зрения обсуждение новых ситуаций полезно. Этим и займёмся.

Пример. В седьмом классе в понедельник не пришли в школу одна девочка и пять мальчиков. При этом число девочек в классе оказалось в 2 раза больше числа мальчиков. Во вторник не пришли один мальчик и девять девочек. При этом число мальчиков оказалось в 1,5 раза больше числа девочек. В среду на уроки пришли все ученики. Сколько школьников присутствовало на уроках в среду в седьмом классе?

Р е ш е н и е.

Первый этап. Составление математической модели.

Пусть х — число девочек, у — число мальчиков в седьмом классе.

В понедельник было (x - 1) девочек, (у - 5) мальчиков. При этом оказалось, что девочек вдвое больше, т. е.

х - 1 = 2(у - 5).

Во вторник было (х - 9) девочек, (у - 1) мальчиков. При этом оказалось, что мальчиков в 1,5 раза больше, т. е.

y - 1 = 1,5 (x - 9).

Математическая модель ситуации составлена:

Второй этап. Работа с составленной моделью.

Сначала упростим каждое уравнение системы.

Для первого уравнения имеем:

x - 1 = 2 (у - 5);

x - 1 = 2у - 10;

х - 2у + 9 = 0.

Для второго уравнения имеем:

y - 1 = 1,5(х - 9);

2(у - 1) = 3(х - 9)

(обе части уравнения умножили на 2); далее

2у - 2 = 3х - 27;

3х - 2у - 25 = 0.

Итак, получили следующую систему двух линейных уравнений с двумя переменными:

(скорректированная математическая модель рассматриваемой ситуации).

Окончание >>>