|
|
|
|
|
Глава 4. Степень с натуральным показателем и её свойства § 15. Что такое степень с натуральным показателемОдна из особенностей математического языка, которым мы с вами должны научиться пользоваться, состоит в стремлении применять как можно более короткие записи. Математик не будет писать а + а + а + а + а, он напишет 5а; не будет писать а + а + а + + а + а + а + а + а + а + а (здесь 10 слагаемых), а напишет 10а; не будет писать Точно так же математик не будет писать 2 • 2 • 2 • 2 • 2, а воспользуется специально придуманной короткой записью 25. Аналогично вместо произведения семи одинаковых множителей 3 • 3 • 3 • 3 • 3 • 3 • 3 он запишет 37. Конечно, в случае необходимости он будет двигаться в обратном направлении, например, заменит короткую запись 2е более длинной 2 • 2 • 2 • 2 • 2 • 2. Если появляется новое обозначение, то возникают и новые термины. И всё это (и обозначения, и термины) охватывается новым определением. Определением обычно называют предложение, разъясняющее суть нового термина, нового слова, нового обозначения. Просто так определения не придумываются, они появляются только тогда, когда в этом возникает необходимость.
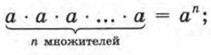
Определение 1. Под аn, где n = 2, 3, 4, 5, понимают произведение п одинаковых множителей, каждым из которых является число а. Выражение аn называют степенью, число а — основанием степени, число n — показателем степени. Подчеркнём ещё раз, что показатель степени — натуральное число (в старших классах мы снимем это ограничение); обычно говорят короче: натуральный показатель. Отсюда и происходит название как всей главы, так и этого параграфа. Итак,
Запись аn читают так: «а в n-й степени». Исключение составляет запись а2, которую читают: «а в квадрате» (хотя можно читать и «а во второй степени»), и запись а3, которую читают: «а в кубе» (хотя можно читать и «а в третьей степени»). Пример 1. Записать в виде степени произведение 5 • 5 • 5 • 5 • 5 • 5 и использовать соответствующие термины. Р е ш е н и е. Поскольку дано произведение шести одинаковых множителей, каждый из которых равен 5, имеем: 5 • 5 • 5 • 5 • 5 • 5 = 56; 56 — степень; 5 — основание степени; 6 — показатель степени. Пример 2. Вычислить (-2)4. Р е ш е н и е. (-2)4 = (-2) • (-2) • (-2) • (-2) = 16. О т в е т: 16.
|
|
|



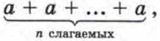 а напишет nа.
а напишет nа.