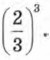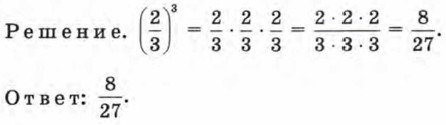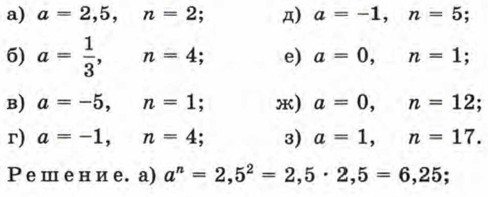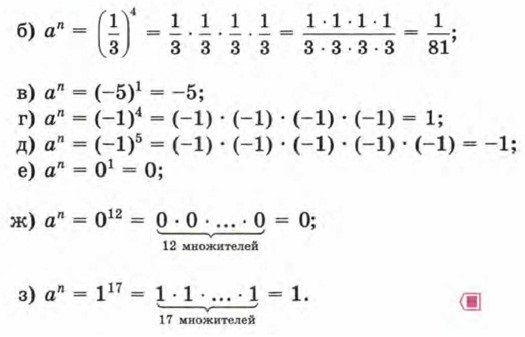§ 15. Что такое степень с натуральным показателем (окончание)

Пример 3. Вычислить

Как вы думаете, полностью ли соответствует названию параграфа определение 1? Параграф называется «Что такое степень с натуральным показателем», т.е. имеется в виду, что в качестве показателя может фигурировать любое натуральное число. А любое ли натуральное число фигурирует в качестве показателя в определении 1? Как вы ответите на этот вопрос?

Ответим на этот вопрос вместе: мы говорили о степени аⁿ, где n = 2, 3, 4, ..., а вот случай, когда n = 1, пока упустили из виду («потеряли» одно натуральное число). Это упущение исправим с помощью нового определения.

Определение 2. Степенью числа а с показателем 1 называют само это число:

а¹ = а.

Пример 4. Найти значение степени аⁿ при заданных значениях аил:

Операцию отыскания степени аⁿ называют возведением в степень. В примере 4 мы рассмотрели восемь случаев возведения в степень.

Пример 5. Вычислить 7¹ • 3² • (-2)³.

Р е ш е н и е. 1) 7¹ = 7;

2) 3² = 3 • 3 = 9;

3) (-2)³ = (-2) • (-2) • (-2) = -8;

4) 7 • 9 • (- 8) = -504.

О т в е т: -504.

В рассмотренных примерах мы несколько раз возводили в степень отрицательные числа. Заметили ли вы закономерность: если отрицательное число возводится в чётную степень, то получается положительное число, если же отрицательное число возводится в нечётную степень, то получается отрицательное число? Попробуйте объяснить, почему это так.

Вопросы для самопроверки

1. Что означает символ аⁿ, где n = 2, 3, 4, ...?

2. Что означает символ а¹?

3. В записи 7⁹ назовите, что является степенью, что основанием степени, что показателем степени.

4. Запишите число 2¹² в виде степени с другим основанием.

<<< К началу