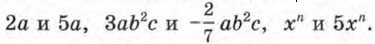§ 21. Сложение и вычитание одночленов

В этой главе мы изучаем новые для вас математические объекты — одночлены. Образно говоря, если для математического языка числа, переменные и степени переменных являются буквами, то одночлены — слогами. Когда в детстве вы учились читать, то сначала изучали буквы, затем читали слоги и только потом целиком произносили написанное слово; буквы, слоги, слова, предложения — этапы изучения языка. И тут уже не важно, нравятся нам одночлены как самостоятельный объект изучения или нет, ничего не поделаешь — без уверенного оперирования ими нам не обойтись, если мы хотим свободно владеть математическим языком.

В § 20 мы ввели понятия одночлена, стандартного вида одночлена. Значит, надо научиться работать с одночленами, например выполнять над ними арифметические операции. При этом сразу договоримся, что будем рассматривать только одночлены, записанные в стандартном виде.

Определение. Два одночлена, состоящие из одних и тех же переменных, каждая из которых входит в оба одночлена в одинаковых степенях (т. е. с равными показателями степеней), называют подобными одночленами.

Примеры подобных одночленов:

Как видите, подобные одночлены отличаются друг от друга только коэффициентами (впрочем, и коэффициенты могут быть равны, например, 7ab и 7ab — подобные одночлены).

А вот примеры неподобных одночленов:

5а и 3а², 2х и 7у, 3а²b² и 6а²b.

Слово «подобные» имеет примерно тот же смысл, что в обыденной речи слово «похожие». Согласитесь, что одночлены 5а²b и 23а²b похожи друг на друга (подобные одночлены), тогда как одночлены 5а²b и 23аb³с² непохожи друг на друга (неподобные одночлены).

Рассмотрим сумму двух подобных одночленов: 5а²b + 23а²b. Воспользуемся методом введения новой переменной: положим а²b = с. Тогда сумму 5a²b + 23а²b можно переписать в виде 5с + 23с. Эта сумма равна 28с. Итак, 5a²b + 23а²b = 28а²b.

В чём смысл этого преобразования? Смысл в том, что равенство 5а²b + 23а²b = 28а²b является верным при подстановке любых значений переменных.

Нам удалось сложить подобные одночлены; оказалось, что это очень просто: достаточно сложить их коэффициенты, а буквенную часть оставить неизменной. Так же обстоит дело и с вычитанием подобных одночленов. Например:

7abc³ - 9abc³ = (7 - 9)abc³ = -2abc³.

А как быть, если одночлены неподобны: можно ли их складывать, вычитать? Увы, пока нельзя! Мы вернёмся к этому вопросу позднее, в главе 6.

Сейчас мы сформулируем алгоритм сложения и вычитания одночленов (впрочем, обычно оставляют только термин «сложение», а знак минус относят к коэффициенту).

Алгоритм сложения одночленов
1. Привести все одночлены к стандартному виду.
2. Убедиться, что все одночлены подобны; если же они неподобны, то алгоритм далее не применяется.
3. Найти сумму коэффициентов подобных одночленов.
4. Записать ответ: одночлен, подобный данным, с коэффициентом, полученным на третьем шаге.

Пример 1. Упростить выражение

2а²b - 7а • 0,5bа + 3b • 2а • (-0,5а).

Р е ш е н и е. Речь идёт о сложении одночленов, значит, будем действовать в соответствии с алгоритмом.

1) Первый одночлен уже имеет стандартный вид.

Для второго одночлена имеем

-7а • 0,5bа = -(7 • 0,5) • (а • а)b = -3,5а²b — это стандартный вид.

Приведём к стандартному виду третий одночлен: 3b • 2а • (-0,5а) = 3 • 2 • (-0,5) • (а • а)b = -3а²b.

2) Получили три одночлена: 2а²b, -3,Ьа²b, -3а²b. Они подобны, поэтому с ними можно производить дальнейшие действия, т. е. переходить к третьему шагу алгоритма.

3) Найдём сумму коэффициентов трёх полученных одночленов: 2 - 3,5 - 3 = -4,5.

4) Запишем ответ: -4,5а²b.

Окончание >>>