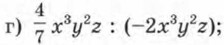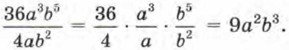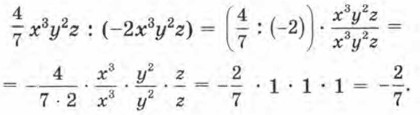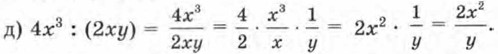§ 23. Деление одночлена на одночлен

Что такое одночлен, мы знаем; как одночлены складывать, вычитать, перемножать и даже возводить в степень — обсудили. Но ведь имеется ещё одна арифметическая операция — деление, операция, обратная умножению. Можно ли быть уверенным в том, что операция деления одночлена на одночлен всегда выполнима — в том смысле, что в частном получится одночлен? Вот об этом и поговорим.

Пример 1. Опираясь на свойства арифметических действий, попытаемся выполнить деление одночленов:

а) 10а : 2;
б) 18ab : (3а);
в) 36а³b⁵ : (4аb²);

д) 4х³ : (2ху);
е) а² : a⁵.

Р е ш е н и е.

а) Воспользуемся тем, что если произведение двух чисел делят на третье число, то можно разделить на это число один из множителей и полученное частное умножить на другой множитель. (Вспомнили? Например, (12 • 4) : 3 = (12 : 3) • 4 = 4 • 4 = 16.) Имеем

10а : 2 = (10 : 2) • а = 5а.

б) Рассуждая как в примере а), получаем

18аb : (3а) = (18 : 3) • (а : а)b = 6 • 1 • b = 6b.

в) 36а³b⁵ : (4аb²) = (36 : 4) • (а3 : а) • (b⁵ : b²) = 9а^{3 - 1} • b^{5 - 2} = 9а²b³.

Иногда удобнее вместо знака деления (:) использовать черту дроби. Вот как тогда будет выглядеть решение примера в):

г) Здесь мы используем комбинированную запись решения, т. е. и знак деления, и черту дроби:

Здесь всё верно, но, как говорят математики, нерационально, поскольку сразу было ясно, что х³у²z : x³y²z = 1 (фактически выражение делится само на себя).

Это не одночлен, значит, разделить 4х³ на 2ху нельзя (в том смысле, чтобы в частном получился одночлен).

е) И эта задача невыполнима, так как мы пока не умеем делить при одном и том же основании степень с меньшим показателем на степень с бо́льшим показателем.

Мы рассмотрели шесть примеров, из них четыре оказались корректными, а два (последние) — некорректными (эти термины мы ввели в § 22).

Проанализируем теперь решённые примеры и попробуем с помощью этого анализа выяснить, когда можно разделить одночлен на одночлен так, чтобы в частном снова получился одночлен.

Естественно, удобнее, чтобы оба одночлена (и делимое, и делитель) были записаны в стандартном виде (впрочем, об этом мы условились ещё в § 21) с отличными от нуля коэффициентами.

Окончание >>>