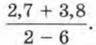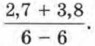§ 22. Умножение одночленов. Возведение одночлена в натуральную степень (окончание)

Р е ш е н и е.

а) 3²а⁵ = 2⁵а⁵ = (2а)⁵. Значит, А = В⁵, где В = 2а.

б) a³b⁶ = a³(b²)³ = (ab²)³. Следовательно, А = В³, где В = ab².

в) Так как 49a²b⁴c⁶ = 7²a²(b²)²(c³)² = (7ab²c³)², то А = В², где В = 7аb²с³.

г) Поскольку -27а³b⁹ = (-3)³a³(b³)³ = (-3ab³)³, заключаем, что А = В³, где В = -3ab³.

д) С одночленом 16а⁸b⁵ у нас ничего не получится. Почему? Давайте рассуждать. Если бы не было множителя Ь5, то задача решалась бы без труда: 16а⁸ = 2⁴(а²)⁴ = (2а²)⁴; если бы вместо b⁵ был множитель, например, b¹², то мы решили бы задачу так:

16a⁸b¹² = 2⁴(а²)⁴(b³)⁴ = (2а²b³)⁴.

Однако множитель b⁵ нельзя представить в виде (b^k)⁴, где k — натуральное число; этот множитель, как говорится, «портит всё дело». Значит, одночлен 16а⁸b⁵ нельзя представить в виде В⁴, где В — некоторый одночлен.

Пример показывает, что в математике далеко не всё получается, не любая задача имеет решение (как и в реальной жизни).

Кстати, если математику предлагают решить задачу, которая явно не имеет решения, то он говорит: «Задача поставлена некорректно» или «Это — некорректная задача». Тот, кто предложил некорректную задачу, должен извиниться. Вот и автор извиняется за пример 4д). Хотя согласитесь, что он был дан не без пользы.

Раз уж мы заговорили о корректных и некорректных задачах, приведём ещё несколько примеров и тех и других, а вы попытайтесь объяснить, почему задача корректна или некорректна.

Корректные задачи

1. Упростить 2аb² • (3аb)³.

2. Упростить 7ab + 8ab + ab.

3. Вычислить

4. Представить одночлен 13а⁴b⁵ в виде суммы одночленов.

5. Представить одночлен 48x³y⁵z в виде произведения одночленов.

6. Представить одночлен А = 25а⁴ в виде квадрата некоторого одночлена В.

Некорректные задачи

1. Сложить одночлены 3ab², 5ab² и 7а²b.

2. Вычислить

3. Представить одночлен А в виде квадрата некоторого одночлена В, если А = -25а⁴.

4. Найти точку пересечения прямых у = -3х + 1 и у = -3x + 5 (см. пример 16) в §10 на с. 61).

1. Как перемножить два одночлена? Приведите пример.

2. Используя переменные р, q и r, составьте одночлен с коэффициентом 144 и представьте его в виде произведения одночленов несколькими способами.

3. Как возвести одночлен в натуральную степень? Приведите пример.

4. Представьте одночлен 16а⁴b⁶ в виде произведения двух одночленов; в виде степени одночлена.

<<< К началу