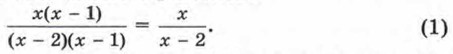|
|
|
|
|
Глава 7. Разложение многочленов на множители § 36. ТождестваВ этом параграфе мы познакомимся ещё с одним алгебраическим термином. Мы знаем, например, что а2 - b2 = (а - b) (а + b), х2 - 4х + 4 = (х - 2)2, (а + b)с = ас + bс.
Написанные равенства верны при любых значениях входящих в их состав переменных. Такие равенства в алгебре называют тождествами. Левую и правую части тождества называют выражениями, тождественно равными друг другу (или просто тождественными). Например, а2 - b2 и (а - b) (а + b) — тождественно равные выражения. Всякую замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения. Всё, чем мы занимались в главах 4—7: действия со степенями, с одночленами, с многочленами, — всё это было изучением тождественных преобразований.
В математике часто бывает так, что, используя некоторый термин, вдруг обнаруживают, что к новой ситуации он оказывается не очень приспособленным, требует уточнения. Это относится и к термину «тождество». Для работы с многочленами данное выше определение абсолютно точное. Однако уже для работы с алгебраическими дробями в понимании этого термина понадобится корректировка, придётся сделать некоторые уточнения. Рассмотрим алгебраическую дробь
Является ли это равенство тождеством? Введя выше этот термин, мы отметили, что тождество — это равенство с переменными, верное при любых значениях переменных. Но про равенство (1) этого сказать нельзя, оно не имеет смысла при х = 1, при х = 2, т. е. оно верно уже не при любых значениях переменной х. Указанные значения не являются допустимыми для выражений, входящих в состав равенства (1). Если же ограничиться только допустимыми значениями переменной х, то при любых таких значениях равенство (1) окажется верным. Учитывая подобные ситуации, математики уточнили понятие тождества.
Определение. Тождество — это равенство, верное при любых допустимых значениях входящих в его состав переменных. В этом смысле равенство (1) — тождество. Вот та корректировка понятия «тождество», о которой мы упоминали выше. Вопросы для самопроверки 1. Что такое тождество? 2. Приведите пример тождества, верного при любых значениях переменных. 3. Приведите пример тождества, верного не при всех, а лишь при допустимых значениях переменных.
|
|
|





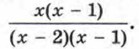 Её можно сократить на х - 1 — на общий множитель числителя и знаменателя. Таким образом, имеет место равенство
Её можно сократить на х - 1 — на общий множитель числителя и знаменателя. Таким образом, имеет место равенство