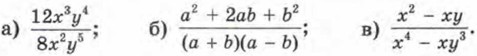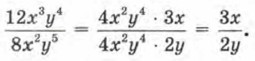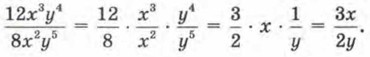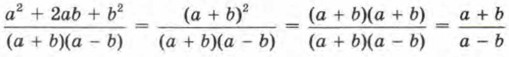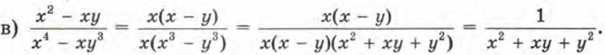|
|
|
|
|
Глава 7. Разложение многочленов на множители § 35. Сокращение алгебраических дробей (окончание)Например, как мы уже установили ранее,
(многочлен 6х3 - 24х2 удалось разделить на 6х2, при этом в частном получается х - 4); мы также отмечали, что
Но так бывает сравнительно редко. Впрочем, похожая ситуация уже встречалась вам — при изучении обыкновенных дробей. Например, дробь Пример. Сократить алгебраическую дробь:
Р е ш е н и е. а) Найдём общий множитель для одночленов 12х3у4 и 8х2у5; это 4х2у4. Тогда 12х3у4 = 4х2у4 • 3х; 8х2у5 = 4х2у4 • 2у. Значит,
Числитель и знаменатель заданной алгебраической дроби сократили на общий множитель 4х2у4. Решение этого примера можно записать по-другому:
б) Чтобы сократить дробь, разложим её числитель и знаменатель на множители. Получим
(дробь сократили на общий множитель а + b). А теперь вернитесь к замечанию 2 из § 1. Видите, данное там обещание мы наконец-то смогли выполнить.
(сократили дробь на общий множитель числителя и знаменателя, т. е. на х(х - у)).
Итак, для того чтобы сократить алгебраическую дробь, следует сначала разложить на множители её числитель и знаменатель (если они не совпадают). Так что ваш успех в этом новом деле (сокращении алгебраических дробей) в основном зависит от того, как вы усвоили материал предыдущих параграфов этой главы. Вопросы для самопроверки 1. Сформулируйте определение алгебраической дроби. 2. Используя переменные а и b, запишите алгебраическую дробь, у которой числитель представляет собой трёхчлен, а знаменатель — одночлен. 3. Что означает задание «Сократите алгебраическую дробь»? Что надо сделать, чтобы выполнить это задание? 4. Может ли в результате сокращения алгебраической дроби в ответе получиться одночлен? число? 5. Приведите пример алгебраической дроби, в результате сокращения которой получается двучлен.
|
|
|



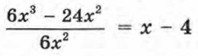
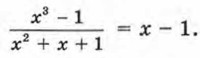
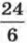 можно заменить целым числом 4, а дробь
можно заменить целым числом 4, а дробь 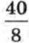 — целым числом 5. Однако дробь
— целым числом 5. Однако дробь 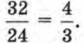 целым числом заменить не удаётся, хотя эту дробь можно сократить, разделив числитель и знаменатель на число 8 — общий множитель числителя и знаменателя:
целым числом заменить не удаётся, хотя эту дробь можно сократить, разделив числитель и знаменатель на число 8 — общий множитель числителя и знаменателя: